Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.11 - Ex. 45
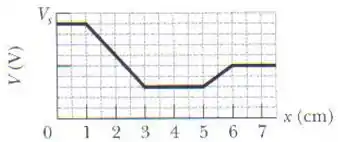
Um próton em um poço de potencial. A figura mostra o potencial elétrico V ao longo de um eixo x. A escala do eixo vertical é definida por . Um próton é liberado no ponto x = 3,5 cm com uma energia cinética inicial de 4,00 eV.
(a) Um próton que está se movendo inicialmente no sentido negativo do eixo x chega a um ponto de retorno (se a resposta for afirmativa, determine a coordenada x do ponto) ou escapa da região mostrada no gráfico (se resposta for afirmativa, determine a velocidade no ponto x = 0)?
(b) Um próton que está se movendo inicialmente no sentido positivo eixo x chega a um ponto de retorno (se a resposta for afirmativa, deterrnine a coordenada x do ponto) ou escapa da região mostrada gráfico (se a resposta for afirmativa, determine a velocidade no ponto x = 6,0 cm)?
Determine
(c) o módulo F e
(d) a orientação (sentido positivo ou negativo do eixo x) da força elétrica a que o próton está submetido quando se encontra ligeiramente à esquerda do ponto x = 3,0 cm. Determine
(e) o módulo F e
(f) a orientação da força elétrica quando o próton se encontra ligeiramente à direita do ponto x = 5,0 cm.
Passo 1
Letra (a)
Em x = 3,5 cm, o próton tem energia potencial 3,0 eV (pois o potencial é 3,0 V). Então a energia total do próton é . Agora pensa comigo: quando o próton atinge o ponto de retorno (se é que atinge), a velocidade é zero. Mas a energia é consante e igual a 7,0 eV, o que significa que o potencial tem que ser 7,0V nesse ponto.
Tem algum ponto do gráfico com 7,0 V? Tem. Tá mais ou menos em x = 1,7cm. É á que ele retorna.
Passo 2
Letra (b)
Na mesma ideia da letra (a), tem algum ponto do gráfico com potencial 7,0 V à direita de x = 3,5 cm? Não, não tem. Então não tem ponto de retorno. Vamos calcular a velocidade em x = 6,0 cm. Conservando a energia:
Convertendo eV para J e substituindo o valor de m, vem .
Passo 3
Letra (c)
Podemos calcular a força pela fórmula . Então precisamos do campo elétrico. Lembra que o valor do campo elétrico é igual à inclinação do gráfico do potencial (ou seja, coefiente angular da reta tangente, ou seja, derivada)? Então vamos calcular essa inclinação entre x = 3,0 cm e x = 1,0 cm:
Então o módulo da força é:
Passo 4
Letra (d)
O campo elétrico aponta para o sentido em que o potencial diminui. No caso, aponta para o sentido positivo do eixo x. Como a carga do próton é positiva, a força também aponta para o sentido positivo do eixo x.
Passo 5
Letra (e)
Na mesma ideia da (c), a gente acha o campo:
Então o módulo da força é:
Passo 6
Letra (f)
Como o potencial aumenta no sentido positivo do eixo x, o campo aponta para o sentido negativo do eixo x e, por isso, a força também aponta para o sentido negativo.
Resposta
Letra (a): 1,7 cm
Letra (b): 20 km/h
Letra (c):
Letra (d): sentido positivo
Letra (e):
Letra (f): sentido negativo