Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 3- Ed: 4º - Capítulo 36.Exercícios e Problemas - Ex. 39

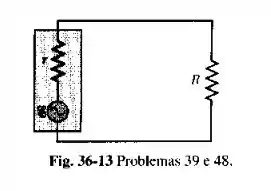
Na Fig. 36- 13 mostre que a taxa média com que a energia é dissipada na resistência R é máxima quando R = r , onde r é a resistência interna do gerador de c a . Até o momento, tínhamos considerado tacitamente que r = 0 .

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Suponha que temos o seguinte circuito, onde r é a resistência interna da fonte CA e R é a resistência externa, a potência média dissipada no resistor R é dada por:

P m é d = I r m s 2 R   ( 1 )

Como o circuito não contém reatâncias, a corrente eficaz é dada por:

I r m s = ε r m s R e q

Onde R e q é a resistência equivalente dos resistores interno e externo, que são conectados em série, então R e q = R + r então:

I r m s = ε r m s R + r

Substitua em (1) para obter:

P m é d = ε r m s R + r 2 R

Passo 2

Para encontrar o valor de R tal que a potência maximize, definimos a derivada de P m é d ,​ em relação a R igual a zero, então:

d P m é d d R = 0

Desenvolvendo os termos

2 R ε r m s R + r - ε r m s R + r 2 + ε r m s R + r 2 = 0

Com isso, temos que

2 R ε r m s R + r 2 = ε r m s R + r

Portanto,

2 R R + r = 1

Isso é somente possível graças

R = r ∴

Resposta

Respondido acima!!!

Exercícios de Livros Relacionados

Remova o indutor do circuito da Fig. 31 - 7 e faça R = 200 Ω , C = 15,0 μ F , f d = 60,0H zeE m = 36,0V . Determine o valor (a) de Z; (b) de ϕ ; (c) de I . (d) Desenhe um diagrama fasorial.
Que resistência R deve ser ligada em série com uma indutância L = 220 m H e uma capacitância C = 12,0 μ F para que a carga máxima do capacitor caia para 99,9 % do valor inicial após 50.0 ciclos? (Supo
Para montar um circuito L C oscilante, você dispõe de um indutor de 10 m H , um capacitor de 5,0 μ F e um capacitor de 2,0 μ F . Determine (a) a menor frequência; (b) a segunda menor frequência: (c) a
Um circuito L C oscilante formado por um capacitor de 1,0 n F e um indutor de 3,0 m H tem uma tensão máxima de 3,0V . Determine (a) a carga máxima do capacitor; (b) a corrente máxima do circuito; (c)
Um indutor é ligado a um capacitor cuja capacitância pode ser ajustada através de um botão. Queremos que a frequência deste circuito L C varie linearmente com o ângulo de rotação do botão, de 2 × 10 5