O bloco de da Figura está preso a um eixo vertical por meio de dois fios. Quando o sistema gira em torno desse eixo, os fios ficam dispostos como indicado no diagrama e a tensão no fio superior é de .
a) Qual é a tensão no fio inferior?
b) Quantas revoluções por minuto o sistema executa?
c) Ache o número de revoluções por minuto para que o fio inferior comece a ficar frouxo.

Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá a seguinte figura que mostra um bloco preso a um eixo vertical por meio de dois fios:
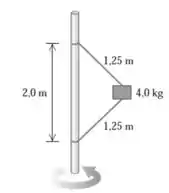
Quando o sistema gira em torno desse eixo, os fios ficam dispostos como indicado no diagrama e a tensão no fio superior é de .
A questão nos faz várias perguntinhas sobre forças e revoluções.
Para isso, utilizaremos a segunda Lei de Newton:
Onde é a força resultante, é a massa e é a aceleração.
Também devemos saber que a força centrípeta é dada por:
Onde é a velocidade e é o raio.
Passo 2
Queremos calcular a tensão no fio inferior.
Para identificar qual é a tensão no fio inferior, vamos a diagrama de forças para o bloco de massa :
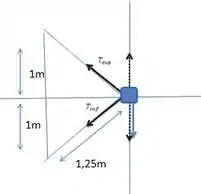
Na vertical o sistema está em equilíbrio e a tensão superior . O ângulo da força tensora com o eixo vertical é o mesmo tanto pra cima, quanto pra baixo.
Vamos descobrir ele. Temos a hipotenusa e o cateto oposto, então pela função cosseno determinar o ângulo:
Passo 3
Agora equacionando as forças na vertical teremos:
Como temos o valor da tensão superior, do ângulo e da massa, podemos determinar a tensão no fio inferior:
Passo 4
Para determinar quantas revoluções o sistema dá por segundo, vamos olhar para as forças na horizontal:
O raio da trajetória não foi dado, mas por Pitágoras podemos determinar:
E como sabemos as tensões nos fios, podemos determinar a velocidade do sistema:
Passo 5
E para determinar o número de revoluções por segundo é só dividir a velocidade por :
E para saber por minuto é só multiplicar por
Passo 6
Quando o fio inferior fica solto, , então o balanço de forças na vertical fica assim:
E a nova tensão superior pode ser calculada:
E com isso podemos, da equação de forças na horizontal, determinar a nova velocidade linear do conjunto:
E da mesma forma que no item anterior, podemos determinar quantas revoluções por segundo o sistema irá fazer:
Passo 7
A tensão na corda superior deve ser maior do que a tensão na corda inferior para que juntos eles produzem uma componente da força resultante vertical para cima para poder contrabalançar a força peso.
Se for menor, o bloco irá cair.