Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 65
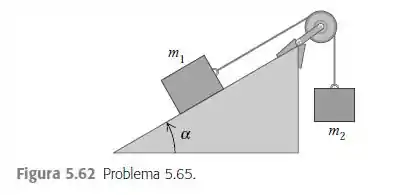
Um bloco de massa está sobre um plano inclinado com um ângulo de inclinação e está ligado por uma corda que passa sobre uma polia pequena a um segundo bloco suspenso de massa (Figura 5.62). O coeficiente de atrito cinético é e o coeficiente de atrito estático é . a) Ache a massa para a qual o bloco de massa sobe o plano com velocidade constante depois que ele entra em movimento. b) Ache a massa para a qual o bloco de massa desce o plano com velocidade constante depois que ele entra em movimento. c) Para que valores de os blocos permanecem em repouso depois de eles serem libertados
a partir do repouso?
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá o seguinte sistema:
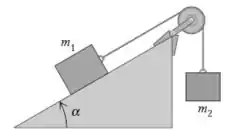
A questão nos diz ainda que o coeficiente de atrito cinético é e o coeficiente de atrito estático é .
Queremos encontrar a massa para a qual o bloco de massa sobe o plano com velocidade constante depois que ele entra em movimento.
Depois, queremos encontrar a massa para a qual o bloco de massa desce o plano com velocidade constante depois que ele entra em movimento.
Por fim, queremos saber para que valores de os blocos permanecem em repouso depois de eles serem libertados a partir do repouso.
Para responder tudo isso, temos que fazer um diagrama de corpo livre do sistema e analisar as forças que estão atuando nos corpos.
Também, utilizaremos também a segunda Lei de Newton:
Onde é a força resultante, é a massa e é a aceleração.
Passo 2
Bom... Nessa questão temos que reparar que ambos os blocos estão unidos por uma corda e submetidos a uma tensão . Além disso, o problema informa que a velocidade constante, então a aceleração é nula.
Quando os blocos estão em movimento, a força de atrito é cinética, , e quando estão parados, a força de atrito é estática, .
Como o sistema está em equilibro, vamos usar a segunda lei de Newton para resolver:
Bora lá!
Passo 3
- A tensão no cabo é contraria a força peso do bloco que está suspenso, logo
- Nesse caso, a força de atrito atua na mesma direção que a tensão no bloco de massa , então só temos que mudar o sinal:
- O equilíbrio aqui será semelhante à análise dos itens (a) e (b), porém o atrito será estático:
Onde é a aceleração da gravidade.
Esta tensão deve superar o atrito e o componente da força gravitacional ao longo da inclinação para o bloco poder se movimentar;
Para encontrar a massa do bloco 2 aplicamos a segunda lei de Newton, no bloco, isso umplica que:
Dividindo tudo por , ficamos com:
Também podemos simplificar mais um pouco, colocando em evidencia:
Passo 4
Passo 5
o maior poderia ser
e o menor poderia ser
.
Resposta
- o maior poderia ser e o menor poderia ser