Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 61
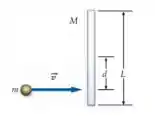
A Figura 10-52 mostra uma barra fina e uniforme, de comprimento e massa , e uma bolinha de massa de modelar de massa . O sistema está sobre uma superfície horizontal sem atrito. A bolinha se move para a direita com a velocidade , atinge a barra a uma distância de seu centro e lá fica grudada. Obtenha expressões para a velocidade do centro de massa e para a rapidez angular do sistema após a colisão.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A barra está parada em pé, com . A bolinha vem com velocidade inicial , bate e fica grudada na barra. Quando ela bate, a tendencia é o conjunto girar em torno do centro de massa do conjunto.
Por isso ele pede a velocidade angular do sistema e o momento angular depois da colisão . Então bora achar esses caras!
Na figura abaixo, podemos observar os diagramas que representam o sistema antes e depois da colisão:
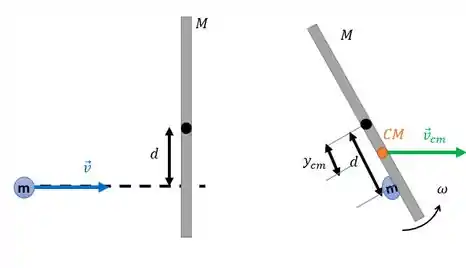
Agora repara que, como não existe torque ou forças externas agindo sobre o sistema, temos que a quantidade de movimento, tanto angular quanto linear são conservadas na colisão. A ideia então é usar esses princípios para chegar em e . Vamos!
Passo 2
O nosso conjunto vai girar em torno do centro de massa dele. Onde está esse centro de massa do conjunto ? Precisamos descobrir!
A barra tinha o centro de massa dela no meio. Mas o conjunto tem um novo centro de massa.
Podemos encontrar a posição do centro de massa novo. Ela vai ser a média ponderada, em relação as massas, das posições do centro de massa da bolinha e da barra.
Nossa origem vai ser no próprio centro de massa da barra. Então o centro de massa da barra é e o da bolinha é
Passo 3
Vamos então usar a conservação de momento angular!
O momento angular inicial da barra é zero porque ela está parada. Já da bolinha pode ser calculado por:
Sendo a massa da bolinha, a velocidade da bolinha e a distância entre o CM e a bolinha.
É importante observar que essa fórmulinha serve para quando e são perpendiculares. Isso acontece quando a bolinha tá quase colando na barra.
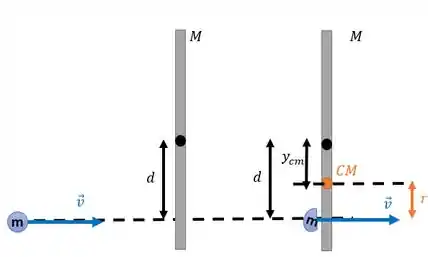
Aí é a distância na barra entre o CM e onde a bolinha bate, ou seja, .
Logo:
Passo 4
Já o momento angular final é o momento do conjunto . Ele pode ser dado por:
O momento de inércia em relação ao centro de massa é dado pela soma dos momentos de inércia da bolinha e da barra em relação ao .
Para a bolinha, a gente pode considerar ela uma partícula:
Sendo a distância entre ela e o , então:
Já para a barra, a gente pode calcular o momento de inércia em relação ao centro da barra (seu centro de massa) e depois usar o teorema dos eixos paralelos:
Sendo que aqui é a distância entre o e o centro da barra:
Somando os dois:
Passo 5
Usando a conservação de momento angular, podemos achar :
Substituindo nossas expressões de e :
Passo 6
E para achar o momento angular final, a gente volta uma casa haha. Lembra que
Então: