Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 81
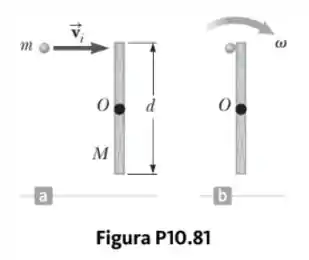
Um projétil de massa move-se para a direita com uma velocidade (Fig. P10.81a). O projétil atinge e gruda em uma extremidade de uma barra fixa de massa , comprimento , articulada sobre um eixo sem atrito perpendicular à página através de (Fig. P10.81b). Gostaríamos de encontrar a variação fracional da energia cinética no sistema em função da colisão.
- Qual é o modelo de análise apropriado para descrever o projétil e a barra?
- Qual é o momento angular do sistema antes da colisão ao redor de um eixo através de ?
- Qual é o momento de inércia do sistema ao redor de um eixo através de O após o projétil ter grudado na barra?
- Se a velocidade angular do sistema após a colisão é , qual é o momento angular do sistema neste instante?
- Encontre a velocidade angular após a colisão em termos das quantidades dadas.
- Qual é a energia cinética do sistema antes da colisão?
- Qual é a energia cinética do sistema após a colisão?
- Determine a variação fracional da energia cinética em função da colisão.
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
Letra a:
O modelo apropriado é para tratar o projétil e a vara como um sistema isolado, não experimentando torque externo, ou força.
Passo 2
Letra b:
Passo 3
Letra c:
Passo 4
Letra d:
Após a colisão, podemos expressar o momento angular como,
Passo 5
Letra e:
Como o momento angular é conservado:
Passo 6
Letra f:
Passo 7
Letra g:
Passo 8
Letra h:
A mudança em energia mecânica é:
Então, a mudança fracionária na energia mecânica é:
Resposta
- Sistema isolado