Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 73

Dois esquiadores no gelo, de massas 55   k g e 85   k g , dão-se as mãos e giram em torno de um eixo vertical que passa entre eles, completando uma volta a cada 2,5   s . Seus centros de massa estão afastados de 1,7   m e o centro de massa dos dois está estacionário. Use o modelo de partícula pontual para cada esquiador e determine (a) a quantidade de movimento angular do sistema em relação a seu centro de massa e (b) a energia cinética total do sistema.

Passo 1

a) Oi pessoal, tudo bem? Vamos analisar essa questão. Queremos o momento angular do sistema formado pelos dois esquiadores.

Por definição a quantidade de movimento angular é dada por:

L = I c m ω

A velocidade angular foi dada. Ele diz que o sistema completa uma volta ( 2 π ) a cada 2,5 s. Podemos escrever então que a velocidade angular em radianos é

ω = 2 π 2,5   r a d / s

Para achar o momento de inércia, temos que encontrar o centro de massa do sistema. Vamos considerar que nossa origem está no CM do esquiador de massa m 2 = 85 k g .

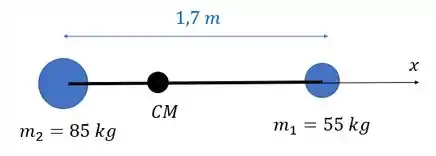
Vamos usar a fórmulinha:

x c m = m 1 x 1 + m 2 x 2 m 1 + m 2

x c m = 55   k g 1,7   m + 85   k g 0 55   k g + 85   k g

x c m = 0,668   m

Passo 2

Podemos, agora, calcular o momento de inércia. Vamos considerar que os esquiadores são partículas. Então o momento de inércia de cada um é dado por

I = M r 2

Onde r é a distância do CM do esquiador para o CM do sistema. Vemos essas distâncias na figura:

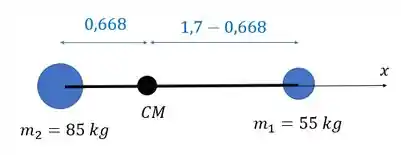
Logo

I c m = m 1 r 1 2 + m 2 r 2 2

I c m = 55   k g 1,7   m - 0,668   m 2 + 85   k g 0,668   m 2

I c m = 96,5   k g ⋅ m 2

Substituindo na equação da quantidade de movimento angular, temos:

L = 96,5 2 π 2,5  

L = 243   J ⋅ s = 0,243   k J ⋅   s

Passo 3

b) A energia cinética associada a quantidade de movimento angular é dada por:

K = L 2 2 I c m

Então vamos só substituir nossos dados aí:

K = ( 243   J ⋅ s ) 2 2 ⋅ ( 96,5   k g ⋅ m 2 )

K = 0,31   k J

Resposta

a )   L = 0 , 243   k J ⋅ s

b ) K = 0,31   k J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um ponto na borda de um rebolo com 0,75m de diâmetro muda de velocidade, a uma taxa constante, de 12m / s para 25m / s em 6,2s . Qual é a aceleração angular média do rebolo?
Em um certo instante, uma partícula de 0,80k g está situada na posição r → = 2,0m i ^ + 3,0m j ^ . O momento linear da partícula está no plano x y e tem um módulo de 2,4k g ∙ m / s e uma direção de 11
Uma partícula de massa M = 0,25k g é liberada de um ponto que está a uma altura h = 1,80m acima do solo e a uma distância s = 0,45m de um ponto de observação O , como mostra a figura. Qual é o módulo
46. Qual é o módulo e qual e a orientação do momentum angular relativo à origem da partícula de 10 0g da FIGURA EX12.47?
48. Qual é o momentum angular da haste de 500g em rotação mostrada na FIGURA EX12.48?