Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 15.Exercícios e Problemas - Ex. 13
A Figura 15.18 mostra dois planos infinitos paralelos, contendo densidades uniformes de carga de mesmo módulo e sinais contrários.
a) Calcule o campo criado pelo sistema.
b) Esboce as linhas de força do campo.
Passo 1
Os resultados desse problema serão muito importantes quando você estudar capacitores de placas paralelas!
Primeiro você precisa lembrar como é o campo elétrico de um único plano infinito:
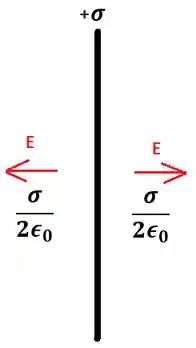
Vemos que o campo é uniforme (não depende da distância para a placa) e seu valor é sempre . Além disso, se a carga do plano for positiva, o campo elétrico apontará para fora da placa.
Da mesma forma, se o plano estiver carregado com uma carga negativa temos um campo “atrativo”:
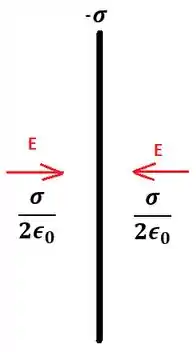
Passo 2
Vamos agora considerar as duas placas juntas:
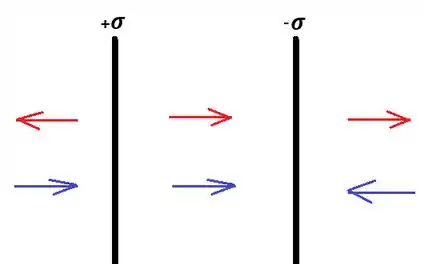
Desenhei em vermelho o campo da placa positiva e em azul o campo da negativa. É fácil perceber que na região externa as placas os campos vão se anular e na região entre as placas eles são se somar.
Com isso, o campo fora da região entre as placas será nulo e o campo entre as placas será
Desta forma,
E como esperado, o campo aponta da placa positiva para a placa negativa.
Passo 3
Como o campo é uniforme entre as placas, as linhas de força serão retas que saem de uma placa e chegam na outra:
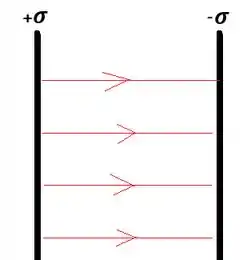
Na região externa as placas não teremos linhas de força para o campo elétrico.