Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 17.Exercícios e Problemas - Ex. 12

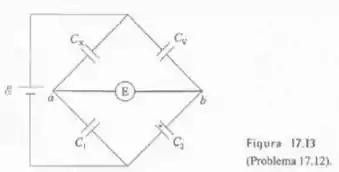
A Figura 17.13 mostra um circuito utilizado para medir capacitâncias, denominado ponte de capacitância. e são dois capacitores de capacitância fixa, é um capacitor de capacitância variável e é o capacitor a ser medido. Uma bateria aplica uma voltagem ao circuito e um eletrômetro mede a diferença de potencial entre os pontos e . O capacitor é sintonizado até que o eletrômetro leia voltagem zero. Mostre que, neste caso, .

Passo 1

Esse problema é bem parecido com o problema de ponte de resistores que será discutido no capítulo 20 do livro e talvez você já tenha visto no ensino médio. Quando a tensão no eletrômetro for nula, os pontos e estarão sob o mesmo potencial elétrico, de modo que

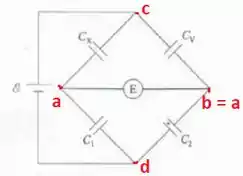
Se for a carga armazenada no capacitor e for a carga armazenada no capacitor , dada a situação do problema, a carga armazenada em será e em será .

Portanto, usando e :

Igualando as expressões:

Isolando :

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada placa de um capacitor com placas paralelas possui uma área igual a 12,2 c m 2 e a distância entre as placas é de 3,28 mm. A carga acumulada em cada placa possui módulo igual a 4,35 × 10 - 8 C . A

Um capacitor de 10μ F com placas paralelas e circulares está ligado a uma bateria de 12,0V . (a) Qual é a carga sobre cada placa? (b) Quanta carga haveria sobre as placas, caso a distância entre elas

Um capacitor é constituído de dois cilindros ocos, co-axiais, de ferro, um dentro do outro. O cilindro interno possui carga negativa e o externo, carga positiva: o módulo da carga sobre cada um é 10,0

Um capacitor esférico é formado por dois condutores esféricos concêntricos separados pelo vácuo. A superfície esférica interna possui raio de 15,0 cm e a capacitância é igual a 116 pF. (a) Qual é o ra

Na figura 24.9a, seja C 1 = 3,0μ F , C 2 = 5,0μ F e V a b = + 52,0V . Calcule (a) a carga em cada capacitor; (b) a diferença de potencial através de cada capacitor.