Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 20.Exercícios e Problemas - Ex. 14

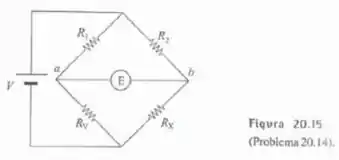
A Figura 20.15 mostra uma ponte de resistência, circuito amplamente utilizado para medida de resistências elétricas. R 1 e R 2 de valor fixo, R V é uma resistência de valor continuamente sintonizável e R X é a resistência a ser medida. Um eletrômetro E mede a diferença de potencial V a b entre os pontos a e b . Mostre que quando V a b é nulo, R X = R 2 R V / R 1 .

Passo 1

Como a tensão medida pelo galvanômetro é nula, temos que

V a = V b

Com isso, a corrente que passa pelo fio central também será nula e nossa ponte de Wheatstone estará em equilíbrio:

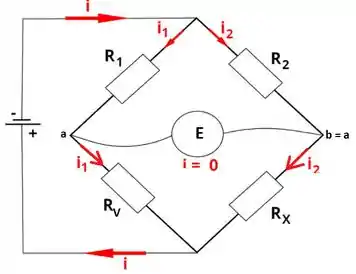
A corrente I 1 que passa por R 1 também passará por R V e a corrente I 2 que passa por R 2 também passará por R X .

Passo 2

A tensão no ramo da esquerda será:

V e s q = R 1 + R V I 1

Já no ramo da direita:

V d i r = R 2 + R X I 2

Igualando as duas tensões:

V = V e s q = V d i r → R 1 + R V I 1 = R 2 + R X I 2

Logo,

I 1 I 2 = R 2 + R X R 1 + R V

Passo 3

Além disso, a ddp no resistor R 1 deve ser igual a ddp no resistor R 2 (eles estão entre os mesmos pontos quando V a b = 0 ):

R 1 I 1 = R 2 I 2 → I 1 I 2 = R 2 R 1

Igualando as relações:

R 2 + R X R 1 + R V = R 2 R 1

Multiplicando em cruz:

R 1 R 2 + R 1 R X = R 1 R 2 + R 2 R V

Logo,

R 1 R X = R 2 R V

Portanto,

R X = R 2 R V R 1

Resposta

R X = R 2 R V R 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a velocidade de arraste em um fio de cobre transportando corrente a uma densidade de 5,0 ⋅ 10 6A m - 2 . A densidade de elétrons de condução no cobre é 8,47 ⋅ 10 28m - 3 .
Uma rede de alta tensão de corrente contínua cobre a distância de 500k m entre a usina geradora e a estação de distribuição. A usina gera uma potência de 5,0G W , a uma voltagem de 500k V . Calcule a
O recorde de mobilidade de um gás de elétrons em um semicondutor foi verificado no GaAs a baixas temperaturas. O valor medido da mobilidade dos elétrons foi 1,1 ⋅ 10 3m 2 / V s . Sendo v - = 1,0 ⋅ 10
Calcule a resistência elétrica entre os pontos a e b da Figura 20.14.
A condutividade elétrica de um cristal é representada no sistema de coordenadas x ,y ,z pela matriz σ = 2,0 1,5 0,5 1,5 3,0 1,0 0,5 1,0 4,0Ω m Calcule a densidade de corrente gerada pelo campo E → = i