Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.6 - Ex. 52

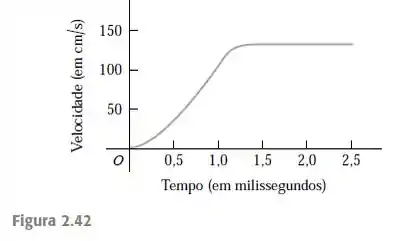
A Figura 2.42 mostra o gráfico de dados coletados de uma pulga saltitante de 210 μ g em um

filme de alta velocidade ( 3500   q u a d r o s / s e g u n d o ). Essa pulga tinha aproximadamente 2   m m de comprimento e saltou a um ângulo de decolagem quase vertical. Use o gráfico para responder a estas perguntas. a) A aceleração da pulga pode chegar a zero? Se sim, quando? Justifique sua resposta. b) Determine a altura máxima que a pulga atingiu nos primeiros 2,5 m s . c) Determine a aceleração da pulga a 0,5 m s , 1,0 m s e 1,5 m s . d) Determine a altura da pulga a 0,5 m s , 1,0 m s e 1,5 m s .

Passo 1

a   ( t ) é a inclinação do gráfico v   v e r s u s   t e a distância percorrida é a área sob o gráfico v   v e r s u s   t .

Podemos esboçar o gráfico da figura 2.42 para facilitar a visualização:

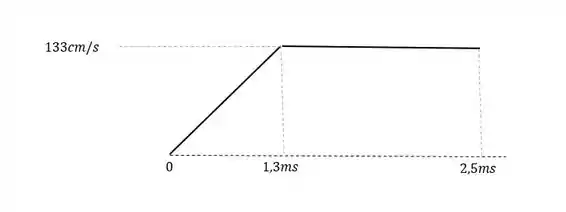
Passo 2

  1. Podemos observar que a inclinação é igual a aceleração, e a aceleração é constante, ou seja, a = 0 para t ≥ 1,3 m s .

    2. Passo 3

  2. Sabemos que a altura máxima, h m á x , é a área debaixo do gráfico v t .

    3. Então, pelo nosso esboço, temos que:

    h m á x ≈ A t r i a n g u l o + A r e t a n g u l o

    Sabemos que a área do triangulo é:

    A t r i a n g u l o = b a s e ⋅ a l t u r a 2

    E que a área do retângulo é:

    A r e t a n g u l o = b a s e ⋅ a l t u r a  

    Então,

    h m á x ≈ 1,3 m s ⋅ 133 c m / s 2 + 2,5 m s - 1,3 m s ⋅ 133 c m / s

    h m á x ≈ 0,25 c m

    Passo 4

  3. a = i n c l i n a ç ã o   d o   g r a f i c o   v t

    4. Sabemos que a aceleração é:

    a = e s p a ç o t e m p o

    Calculando a área em cada instante de tempo, t :

    a ( 0,5 m s ) ≈ a ( 1,0 m s ) ≈ 133 c m / s 1,3 m s = 1,0 × 10 5 c m / s 2

    a 1,5 m s = 0

    Pois a inclinação é zero.

    Passo 4

  4. Sabemos que a altura é igual a área:

h = á r e a   d e b a i x o   d o   g r á f i c o  

Para t = 0,5 m s :

h 0,5 m s ≈ A t r i a n g u l o = 0,5 m s ⋅ 33 c m / s 2 = 8,3 × 10 - 3 c m

Para t = 1,0 m s :

h 0,5 m s ≈ A t r i a n g u l o = 1,0 m s ⋅ 133 c m / s 2 = 5,0 × 10 - 2 c m

Para t = 1,5 m s :

h 1,5 m s ≈ A t r i a n g u l o + A r e t a n g u l o = 1,3 m s ⋅ 133 c m / s ⋅ 0,2 m s ⋅ 1,3 m s 2 = 0,11 c m

Resposta

  1. a = 0
  2. h m á x ≈ 0,25 c m
  3. a ( 0,5 m s ) ≈ a ( 1,0 m s ) ≈ 1,0 × 10 5 c m / s 2 e a 1,5 m s = 0
  4. h 0,5 m s = 8,3 × 10 - 3 c m

h 0,5 m s = 5,0 × 10 - 2 c m

h 1,5 m s = 0,11 c m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A FIGURA P 2.24 mostra o diagrama de movimento, feito a dois quadros de filme por segundo, de uma bola rolando em um trilho. Este possui um trecho pegajoso com de 3,0 m de comprimento. a. Use uma régu
A aceleração de uma partícula é descrita pela função a x = 10 - t m / s 2 , onde t está em s. Suas condições iniciais são x 0 e v 0 x 0m / s em t = 0 .a. Em que instante a velocidade volta a ser nula?
A velocidade de uma partícula é descrita pela função v x = k t 2m / s , onde k é uma constante e t está em s. A posição da partícula em t 0 = 0s é x 0 = - 9,0m . Em t 1 = 3,0s ela se encontra em x 1 =
Um bloco suspenso por uma mola é puxado para baixo e solto. O gráfico da posição versus tempo do bloco é mostrado na FIGURA P2.29. a. Em que instantes a velocidade é nula? Em que instantes ela é mais
A posição de uma partícula é dada por x = ( 2 t 3 - 9 t 2 + 12 )m , onde t está em s. a. Em que instante ou instantes v x é nula?b. Quais são a posição e a aceleração da partícula neste(s) instante(s)