Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 24.Exercício - Ex. 18

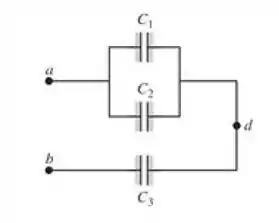
Na figura 24.26, seja C 1 = 6,0 μ F , C 2 = 3,0 μ F e C 3 = 5,0 μ F . O circuito de capacitores está conectado a um potencial aplicado V a b . Quando as cargas dos capacitores atingem os seus valores finais, a carga em C 2 é igual a 4,0 μ C . (a) Quais são as cargas nos capacitores C 1 e C 3 ? (b) Qual é a voltagem aplicada V a b ?

Passo 1

Temos para associação de capacitores:

i ) C a p a c i t o r e s   e m   p a r a l e l o :

C 12 = C 1 + C 2

Q 12 = Q 1 + Q 2

V 1 = V 2 = V 12

i i ) C a p a c i t o r e s   e m   s é r i e :

1 C e q = 1 C 12 + 1 C 3

Q 12 = Q 3 = Q

V = V 12 + V 3

Passo 2

letra a)

Queremos as cargas de C 1 e C 3 .

Sabemos que V 1 = V 2 , então podemos escrever essas voltagens em termos das capacitâncias e das cargas.

V 1 = V 2

Q 1 C 1 = Q 2 C 2

Q 1 = C 1 Q 2 C 2

Q 1 = 6 ⋅ 10 - 6   ⋅ 4 ⋅ 10 - 6   3 ⋅ 10 - 6  

Q 1 = 8 ⋅ 10 - 6   C

Passo 3

Como capacitores em série têm as cargas iguais:

Q 3 = Q 12 = Q 1 + Q 2

Q 3 = 8 ⋅ 10 - 6   + 4 ⋅ 10 - 6  

Q 3 = 12 ⋅ 10 - 6     C

Passo 4

letra b)

Queremos agora descobrir a voltagem total V a b .

Podemos escrever então:

V a b = V 12 + V 3

Sendo que V 1 = V 2 = V 12 . Logo:

V a b = V 1 + V 3

Podemos substituir os potenciais já que sabemos as cargas e as capacitâncias.

V a b = Q 1 C 1 + Q 3 C 3

V a b = 8 ⋅ 10 - 6   6 ⋅ 10 - 6   + 12 ⋅ 10 - 6   5 ⋅ 10 - 6  

V a b = 1,33 + 2,4

V a b = 3,73   V

Resposta

letra a) Q 1 = 8 ⋅ 10 - 6   C , Q 3 = 12 ⋅ 10 - 6     C

letra b) V a b = 3,73   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um capacitor de 10μ F com placas paralelas e circulares está ligado a uma bateria de 12,0V . (a) Qual é a carga sobre cada placa? (b) Quanta carga haveria sobre as placas, caso a distância entre elas
Um capacitor é constituído de dois cilindros ocos, co-axiais, de ferro, um dentro do outro. O cilindro interno possui carga negativa e o externo, carga positiva: o módulo da carga sobre cada um é 10,0
Um capacitor esférico é formado por dois condutores esféricos concêntricos separados pelo vácuo. A superfície esférica interna possui raio de 15,0 cm e a capacitância é igual a 116 pF. (a) Qual é o ra
Na figura 24.9a, seja C 1 = 3,0μ F , C 2 = 5,0μ F e V a b = + 52,0V . Calcule (a) a carga em cada capacitor; (b) a diferença de potencial através de cada capacitor.
Um capacitor de 10,0 μ F com placas paralelas é ligado a uma bateria de 12,0 V. Quando o capacitor está plenamente carregado, a bateria é desconectada sem que haja qualquer perda de carga nas placas.