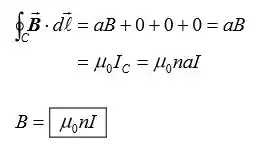Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 27.1 - Ex. 50
A Figura 27-57 mostra um solenóide que tem n voltas por unidade de comprimento e carrega uma corrente I. Aplique a lei de Ampère à curva retangular mostrada na figura para derivar uma expressão para a magnitude do campo magnético. Suponha que dentro do solenóide o campo magnético seja uniforme e paralelo ao eixo central, e que fora do solenóide não haja campo magnético.
Passo 1
Eae galera! Tudo tranquilo? Expresse a integral em torno do caminho fechado C como a soma das integrais ao longo dos lados do retângulo:
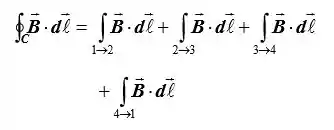
Calculando:
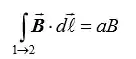
Passo 2
Para os caminhos 2 → 3 e 4 → 1, B r é zero (fora do solenóide) ou é perpendicular a l r d e assim:
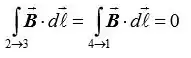
Passo 3
Substitua na lei de Ampère para obter:
Resposta
Exercícios de Livros Relacionados
Um solenóide de 300 voltas tem raio igual a 2c m e comprimento de 25c m ; um solenóide de 1000 voltas tem raio igual a 5c m e também 25 c m de comprimento. Os dois solenóides são coaxiais, estando um
Um longo solenoide tem n voltas por unidade de comprimento e conduz uma corrente que varia com o tempo de acordo com I = I 0 ⋅ s e n ω t . O solenoide tem seção transversal circular de raio R . Determ
Como um técnico em eletricidade, você está projetando um grande solenoide para produzir um campo magnético uniforme de 0,150 T próximo ao centro do solenoide. Você possui fio suficiente para 4.000 esp
Um solenoide com 35 cm de comprimento contendo 450 bobinas circulares com 2,0 cm de diâmetro conduz uma corrente de 1,75 A. (a) Qual é o campo magnético no centro do solenoide, a 1,0 cm das bobinas? (
Um solenoide toroidal tem raio interno de 12,0 cm e raio externo de 15,0 cm. Ele conduz uma corrente de 1,50 A. Quantas voltas igualmente espaçadas ele precisa ter para que produza um campo magnético