Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.2 - Ex. 20

Na figura 29-50, duas espiras circulares concêntricas, que conduzem correntes no mesmo sentido, estão no mesmo plano. A espira 1 tem 1,50   c m de raio e conduz uma corrente de 4,00   m A . A espira 2 tem 2,50   c m de raio e conduz uma corrente de 6,00   m A . O campo magnético B → no centro comum das duas espiras é medido enquanto se faz girar a espira 2 em torno de um diâmetro. Qual deve ser o ângulo de rotação da espira 2 para que o módulo do campo B → seja 100   n T ?

Passo 1

E aí, pessoal! 😉

Nesse problema temos duas espiras circulares concêntricas, que conduzem correntes no mesmo sentido, estão no mesmo plano. A espira 1 tem 1,50   c m de raio e conduz uma corrente de 4,00   m A . A espira 2 tem 2,50   c m de raio e conduz uma corrente de 6,00   m A . A espira 2 gira em torno de um diâmetro e nosso objetivo é saber qual deve ser o ângulo de rotação da espira 2 para que o módulo do campo B → seja 100   n T .

Parece complicado? 👀

Primeira coisa que temos que lembrar é a Regra da mão direita, por essa regra, descobrimos que o campo magnético B gerado pela circulação de corrente I em uma espira circular é perpendicular ao raio da espira. Olha pra essa imagem:

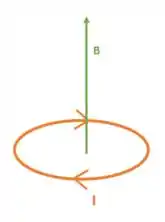
Mas quanto vale o campo magnético B ? Para calcular, usamos a seguinte equação:

B =   μ   . I 2 r

Onde:

  • I é a corrente que circula pela espira;
  • r é o raio da espira e
  • μ é a permeabilidade magnética do meio, no caso igual a μ = 4 .   π   .   10 - 7   T . m / A .

Bora lá! 😁

Passo 2

Logo vamos calcular o campo de cada espira! Para a espira 1, nós temos os seguintes dados:

  • Raio r 1 =   1,50   c m = 1,5   .   10 - 2 m  
  • Corrente I 1 =   4,00   m A = 4 .   10 - 3 A

    • Substituindo os valores na fórmula:

    B 1 =   ( 4 .   π   .   10 - 7   T . m A )   . ( 4 .   10 - 3 A ) 2 . ( 1,5   .   10 - 2 m )

    Logo:

    B 1 =   ( 4 .   π   .   10 - 7   T . m A )   . ( 4 .   10 - 3 A ) 2 . ( 1,5   .   10 - 2 m )

    B 1 = 50,2655   .   10 - 10 3   .   10 - 2 T

    B 1 = 168   n T

    Fazendo o mesmo para a espira 2, vamos ter os seguintes dados:

  • Raio r 2 =   2,50   c m = 2,5   .   10 - 2 m  
  • Corrente I 2 =   6,00   m A = 6 .   10 - 3 A

Substituindo os valores na fórmula:

B 2 =   4 .   π   .   10 - 7   T . m A . 6 .   10 - 3 A 2 . 2,5   .   10 - 2 m

B 2 =   75,398   .   10 - 10 5   .   10 - 2 T

B 2 =   75,398   .   10 - 10 5   .   10 - 2 T

B 2 =   151   n T

Tranquilo até aqui? 😊

Passo 3

Nós descobrimos os valores dos campos magnéticos gerados pelas espiras B 1 e B 2 , mas vamos entender como eles se somam. Primeiro, se não tiver ângulo nenhum, nós temos essa imagem:

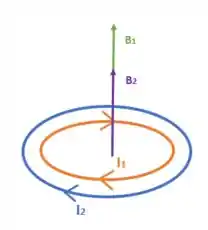
Quando giramos a espira 2, giramos o campo B 2 o mesmo ângulo, ficaremos com algo dessa forma:

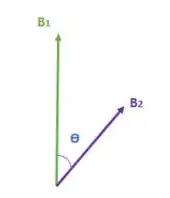
Usando a lei dos cosenos para soma de dois vetores (lembrando que aqui o sinal é + ), vamos descobrir a soma desses vetores B 2 e B 1 :

B 2 =   B 1 2 + B 2 2 + 2   .   B 1   .   B 2   .   c o s θ

A condição que desejamos é que B = 100   n T , logo podemos substituir esse valor na equação, assim como os valores que calculamos para os campos que compõem esse campo resultante:

( 100   n T ) 2 = 168   n T 2 + 151 n T 2 + 2   .   ( 168   n T )   .   ( 151   n T )   c o s θ

Elevando os campos ao quadrado e realizando as multiplicações:

100 × 10 - 9 2 = 28.224 × 10 - 15 + 28.801 × 10 - 15 + 50.736 × 10 - 15 c o s θ

Somando as componentes elevadas ao quadrado:

10 × 10 - 15 = 57.025 × 10 - 15 +   50.736 × 10 - 15 c o s θ

Isolando o cosseno:

- 50.736 × 10 - 15 .   c o s θ = 57.025 × 10 - 15 - 10 × 10 - 15

c o s θ = 57.025 × 10 - 15 - 10 × 10 - 15 - 50.736 × 10 - 15

c o s θ = 41.025 × 10 - 15 - 50.736 × 10 - 15  

θ = a r c c o s ⁡ ( - 0.808597 )

Logo, achamos o ângulo:

θ ≅ 143.96 °

E aí! entendeu tudo? Responde Aí! 😇

Resposta

O ângulo é igual a:

θ ≅ 144 °    

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

54- Na Figura 28.51 , a ramificação da bateria no circuito está muito distante dos dois segmentos horizontais que contêm dois resistores. Esses segmentos horizontais estão separados por uma distância
61- Tome como referência a situação descrita no Problema 28.60 . Considere um terceiro fio longo paralelo aos outros dois primeiros passando pelo ponto P (Figura 28.54 ) e suponha que cada fio conduza
57- Uma carga puntiforme negativa q = - 7.20m C se move em relação a um sistema de referência. Quando a carga puntiforme está na origem, o campo magnético que ela produz no ponto x = 25.0c m ,y = 0 ,z
51- Duas cargas puntiformes, q = + 8.0 μ C e q ' = - 5.0μ C se movem em relação a um sistema de referência como indicado na Figura 28.50 com velocidades v = 9.0 × 10 4m / s e v ' = 6.50 × 10 4m / s .
60- A Figura 28.54 representa o plano x y que corta perpendicularmente dois fios longos e paralelos que conduzem uma corrente I , de mesmo módulo, porém de sentidos contrários. ( a ) Copie o diagrama