Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.2 - Ex. 15
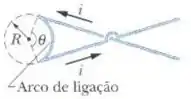
A figura 29-52 mostra um fio que conduz uma corrente . Dois trechos retilíneos semi-infinitos, ambos tangentes à mesma circunferência são ligados por um arco de circunferência que possui um ângulo central e coincide com a parte da circunferência. O arco e os dois trechos retilíneos estão no mesmo plano. Se no centro da circunferência, qual é o valor de ?
Passo 1
E aí, galerinha! 😎
Nesse problema temos um fio que conduz uma corrente . Dois trechos retilíneos semi-infinitos, ambos tangentes à mesma circunferência são ligados por um arco de circunferência que possui um ângulo central e coincide com a parte da circunferência. O arco e os dois trechos retilíneos estão no mesmo plano. Se no centro da circunferência queremos saber qual é o valor de .
Tem ideia de como fazemos isso? 🤔
De acordo com a equação do fio retilíneo semi-infinito , a contribuição da corrente em cada fio semi-infinito para o campo magnético no centro da circunferência é
E em ambos os casos, o campo aponta para fora do papel.
De acordo com a equação do campo magnético para um arco circunferência, a contribuição da corrente no arco de circunferência para o campo magnético no centro da circunferência é
E o campo aponta para dentro do papel.
Veja só! 😉
Passo 2
Igualando a zero o campo magnético total no centro da circunferência, temos:
Substituindo as equações do passo anterior...
Multiplicando os dois lados por , temos
E aí! entendeu tudo? Responde Aí! 😉
Resposta
O valor do ângulo é igual a: