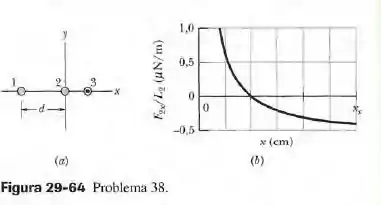
A figura 29-64a mostra, em seção reta, três fios percorridos por corrente que são longos, retilíneos e paralelos. Os fios 1 e 2 são mantidos fixos no eixo x , separados por uma distância d . O fio 1 conduz uma corrente de 0,750A , mas o sentido da corrente é desconhecido. O fio 3, com uma corrente de 0,250A para fora do papel pode ser deslocado ao longo do eixo x , o que modifica a força F 2 → a que está sujeito o fio 2. A componente x dessa força é F 2 x e o seu valor por unidade de comprimento do fio 2 é F 2 x / L 2 . A figura 29-64b mostra o valor de F 2 x / L 2 em função da coordenada x do fio 3. O gráfico possui uma assíntota F 2 x L 2 = - 0,627 μ N / m para x → ∞ . A escala horizontal é definida por x s = 12,0c m . Determine (a) o valor e (b) o sentido (para dentro ou para fora do papel) da corrente no fio 2.

i 2 = 0,50A ;O sentido de i 2 é para fora do papel.

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.3 - Ex. 40

A figura 29-64a mostra, em seção reta, três fios percorridos por corrente que são longos, retilíneos e paralelos. Os fios 1 e 2 são mantidos fixos no eixo , separados por uma distância . O fio 1 conduz uma corrente de , mas o sentido da corrente é desconhecido. O fio 3, com uma corrente de para fora do papel pode ser deslocado ao longo do eixo , o que modifica a força a que está sujeito o fio 2. A componente dessa força é e o seu valor por unidade de comprimento do fio 2 é . A figura 29-64b mostra o valor de em função da coordenada do fio 3. O gráfico possui uma assíntota para . A escala horizontal é definida por . Determine (a) o valor e (b) o sentido (para dentro ou para fora do papel) da corrente no fio 2.

Passo 1

Observando o gráficco da figura 29-64b, vemos que ele passa pelo zero, o que significa que as corrente nos fios 1 e 3 exercem forças em sentidos opostos sobre o fio 2. Com osabemos que o sentido da corrente no fio 3 é para fora do papel, isso significa que o sentido da corrente 1 também é para fora do papel. Qual o fio 3 está a uma grande distância do fio 2, o único campo a que o fio 2 está sbmetido é o produzido pela corrente do fio 1; neste caso, de acordo com o gráfico da figura 29-64b, a força é negativa. Isso significa que o fio 2 é atráido pelo fio 1, o que indica que o sentido da corrente no fio 2 é o mesmo da corrente do fio 1, ou seja, para fora do papel.

Passo 2

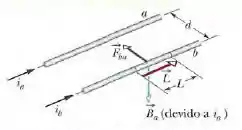
A força entre duas correntes paralelas na presença do campo magnético externo é dada por:

em que é o vetor comprimento do fio. Podemos ver na figura acima, os vetores e são mutuamente perpendiculares e, portanto, de acordo com a equação para fios retilíneos longos, podemos escrever:

Passo 3

Conforme o enunciado, com o fio 3 a uma distância infinita do fio 2, a força por metro é , o que nos permite escrever:

Quando ofio 3 está no ponto , a força é nula e, portanto:

Substituindo pelo seu valor na expressão que encontramos anteriormente, obtemos:

Resposta

;
O sentido de é para fora do papel.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que o módulo do campo magnético produzido no centro de uma espira retangular de comprimento L e largura W , percorrida por uma corrente i , é dado por: B = 2 μ o i π ⋅ L 2 + W 2 1 2 L W

Uma espira quadrada de lado a conduz uma corrente i , Mostre que, no centro da espira, o módulo do capo elétrico produzido pela corrente é B = 2 2 μ 0 i π a

Na figura 29-64, cinco fios paralelos longos no plano x y estão separados por uma distância d = 50c m . As correntes para dentro do papel são i 1 = 2,00A , i 3 = 0,250A , i 4 = 4,00A e i 5 = 2,00A ; a

Um físico deseja produzir ondas eletromagnéticas com frequência igual a 3,0 THz (1 THz=1 terahertz= 10 12 Hz) usando um magnétron (veja o Exemplo 27.3). (a) Qual é o campo magnético necessário? Compar

Campos E e B perpendiculares. Uma partícula com velocidade inicial v 0 _ = ( 5,85 × 10 3 m / s ) j ^ entra em uma região com campos elétrico e magnético uniformes. O campo magnético na região é B _ =