A figura 29-66 mostra uam seção reta de um fio cilíndrico longo de raio que conduz uma corrente uniforme de . Determine o móulo do campo magnético produzido pela corrente a uma distância do eixo do fio igual a (a) ; (b) ; (c) (superfície do fio) e (d) .

Passo 1
A lei de Àmpere é utilizada para determinar o campo magnético total de uma região que apresente algum tipo de simetria. De acordo com ela:
O círculo do sinal de integral indica que a integração do produto escalar deve ser realizada para uma curva fechada, conhecida como amperiana. A corrente é a corrente total envolvida pela curva fechada. Essa corrente tamém pode ser escrita como:
onde é a densidade de corrente na curva fechada.
A brincadeira aqui vai ser usar a lei de ampére e a equação da densidade de corrente pra chegarmos numa equação pro campo magnético dependente do raio da superfície amperiana, fazendo isso vamos só substituir o raio pra cada um dos itens pedidos. A única situação diferente é caso a amperiana esteja fora do fio, daí usaremos outra equação.
Passo 2
Vamos então correr atrás desse campo magnético aí!
Para determinarmos o campo magnético em pontos situados no interior do fio, podemos usar uma amperiana de raio por dentro do fio, conforme a figura abaixo.
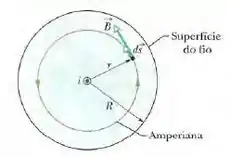
Vamos então usar lei de ampére por aqui, se você integrar o campo ao longo do comprimento fechado da superfície do fio, terá o resultado do comprimento de uma circuinferência, então a lei de ampére vai ficar:
Para calcular o lado direito da lei de Àmpere, observamos que, como a distribuição de corrente é uniforme, a corrente envolvida pela amperiana é proporcional à área envolvida pela curva, ou seja,
Então vamos substituir essa equação da corrente envolvida pela amperiana na segunda parte da lei de ampére.
Então unindo as parcelas temos:
Onde é o raio da amperiana e é o raio da seção transversal do fio, repara que somente varia na questão e aqui já podemos responder o item a. pois quando , temos:
Essa equação acima define o campo se a amperiana estiver dentro do fio! Caso ela esteja fora usaremos.
Onde é o raio da amperiana, beleza?
Passo 3
Vamos então para a nossa brincadeira, já temos a expressão que vamos usar aqui:
Aqui é substituir a corrente e o raio , lembrando que esse raio é constante assim como a corrente.
Para ,
Passo 4
O passo 4 segue o mesmo flow:
Aqui é substituir a corrente e o raio , lembrando que esse raio é constante assim como a corrente.
Para :
Passo 5
No item d. estamos fora da amperiana pois.
Então usaremos.
Aqui é substituir a corrente e o raio que não é constante nesse caso, estamos fora da amperiana.
Para ,
Resposta
- ;
- ;
- .