Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.Problemas Adicionais - Ex. 78
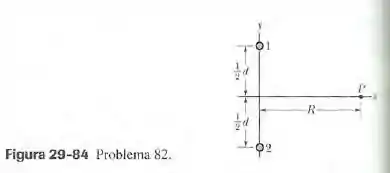
A figura 29-84 mostra, em seção reta, dois fios longos paralelos separados por uma distÂncia . A corrente nos fios é , para fora do papel no fio 1 e para dentro do papel no fio 2. Em termos dos vetores unitários, qual é o campo magnético no ponto P situado a uma distância da reta que liga os dois fios?
Passo 1
Para descobrirmos a distância dos fios para o ponto , vamos aplicar o famoso teorema de pitágoras. Temos que os catetos valem e . Assim,
As componentes verticais dos campos se cancelam e as componentes horizontais se somam, apontando no sentid positivo do eixo . O resultado final é:
O que nos dá, na notação dos vetores unitários, .
Resposta
O campo magnético no ponto P é:
Exercícios de Livros Relacionados
Na figura 29-43, o ponto P 1 está a uma distância R = 13,1c m do ponto médio de um fio retilíneo de comprimento L = 18,0c m que conduz uma corrente i = 58,2m A . (Observe que o fio não é longo) Qual é
Um fio longo está sobre o eixo x e conduz uma corrente de 30A no sentido positivo do eixo x . Um segundo fio longo é perpendicular ao plano x y , passa pelo ponto ( 0 ; 4,0m ; 0 ) e conduz uma corrent
Na figura 29-47, parte de um fio longo isolado que conduz uma corrente i = 5,78m A é encurvada para formar uma espira circular de raio R = 1,89c m . Em termos dos vetores unitários, determine o campo
Na figura 29-47, parte de um fio longo isolado que conduz uma corrente i = 5,78m A é encurvada para formar uma espira circular de raio R = 1,89c m . Em termos dos vetores unitários, determine o campo
Uma corrente é estabelecida em uma espira constituída por uma semicircunferência de 4,00c m de raio, uma semicircunferência concêntrica de raio menor e dois segmentos retilíneos radiais, todos no mesm