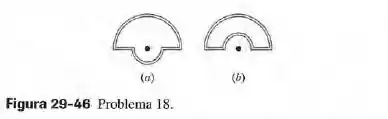
Uma corrente é estabelecida em uma espira constituída por uma semicircunferência de de raio, uma semicircunferência concêntrica de raio menor e dois segmentos retilíneos radiais, todos no mesmo plano. A figura 29-46ª mostra o arranjo, mas não está desenhada em escala. O módulo do campo magnético produzido no centro da curvatura é . Quando a semicircunferência menor sofre uma rotação de (figura 29-46b), o modulo do campo magnético produzido no centro de curvatura diminui para e o sentido do campo se inverte. Qual é o raio da semicircunferência menor?

No primeiro caso temos ; no segundo, . Sabemos que e . Dividindo as equações iniciais uma pela outra e cancelando fatores comuns, temos:

O que nos dá:

Como , temos: