Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.4 - Ex. 9
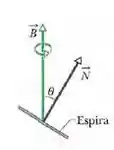
Na figura 30-42, uma espira circular com de diâmetro (vista de perfil) é posicionada com a normal fazendo um ângulo com a direção de um campo magnético uniforme cujo módulo e . A espira começa a girar de tal forma que descreve um cone em torno da direção do campo à taxa de revoluções por minuto; o ângulo permanece constante durante o processo. Qual é a força eletromotriz induzida na espira?
Passo 1
Fala aí, pessoal! 😉
Nesse problema temos uma espira circular com de diâmetro que é posicionada com a normal fazendo um ângulo com a direção de um campo magnético uniforme cujo módulo e . A espira começa a girar de tal forma que descreve um cone em torno da direção do campo à taxa de revoluções por minuto; o ângulo permanece constante durante o processo. A partir daí queremos saber qual é a força eletromotriz induzida na espira.
Tem ideia de como fazemos isso? 🤔
Bom, galera, a Lei de Lenz veio logo após a lei de Faraday (aquela da indução, lembram?). Um cara chamado Heinrich Friedrich Lenz prôpos uma regra, hoje ocnhecida como Lei de Lenz, para determinar o sentido da corrente induzida em uma espira: a corrente induzida em uma espira tem um sentido tal que o campo magnético produzido pela corrente se opõe ao campo magnético que induz. Assim, a força eletromotriz induzida tem o mesmo sentido que a corrente induzida.
Bacana, não é? 😉
Passo 2
Na nossa questão temos uma uma espira girando em torno da direção do campo.
Observe que a área pela qual o campo passa da espira não muda, o que nos leva a concluir que não ocorre variação de fluxo, uma vez que:
Assim, como o fluxo magnético na espira é constante, a força eletromotriz induzida nessa espira é zero pela lei de Faraday!
E aí! o que achou? Responde Aí! 😉
Resposta
A força eletromotriz induzida é igual a zero.