Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.5 - Ex. 35
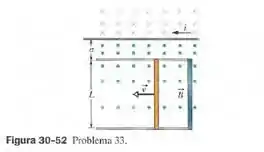
A figura 30-52 mostra uma barra de comprimento que é forçada a se mover com velocidade escalar constante ao longo de trilhos horizontais. A barra, os trilhos e a fita metálica na extremidade direita dos trilhos formam uma espira condutora. A barra tem uma resistência de ; a resistência do resto da espira é desprezível. Uma corrente que percorre um fio longo, situado a uma distância da espira produz um campo magnético (não uniforme) que atravessa a espira. Determine (a) a força eletromotriz e (b) a corrente induzida da espira. (c) Qual é a potência dissipada na espira? (d) Qual é o módulo da força que deve ser aplicada à espira para que se mova com velocidade constante? (e) Qual é a taxa com a qual a força realiza trabalho sobre a espira?
Passo 1
E aí, pessoal! 😉
Nesse problema temos o classico caso da barra condutora que desliza em dois trilhos.
Um fio condutor passa a uma distancia do sistema e é percorrido por uma corrente .
Queremos saber a , a corrente, a potência dissipada, força e seu trabalho na espira.
Tem ideia de como fazemos isso? 🤔
Vamos chamar de a distância entre a barra e a extremidade direta dos trilhos. O campo produzido pelo fio em um ponto do espaço é , na qual é a distância entre o ponto e o fio. Considere uma tira horiontal infinitesimal de comprimento e largura , situada a uma distância do fio. O fluxo através da tira é:
Assim, o fluxo magnético que atravessa a espira formada pela barra e pelos trilhos é dado por:
Tranquilo até aqui? 😉
Passo 2
O módulo da força eletromotriz induzida em uam espira condutora é igual à taxa de variação com o tempo do fluxo magnético que atravessa a espira. A expressão para caluclar a força eletromotriz é a seguinte:
O sinal negativo mostra que a força eletromotriz se opõe à variação do fluxo.
Fazendo uso da lei de Faraday para essa questão, temos:
Bacana, não é? 😬
Passo 3
De acordo com a primeira lei de Ohm,
Como o fluxo está aumentando, o campo magnético produzido pela corrente induzida aponta para dentro do papel na região envolvida pela barra e pelos trilhos e, portanto, a corrente tem o sentido horário.
Já a potência dissipada na espira é dada por:
Está acompanhando? 😁
Passo 4
Para que a barra se mova com velocidade constante, a resultante das forças que agem sobre a barra eve ser nula. Para isso, a força externa aplicada à barra deve ser igual, em módulo, à força magnética e deve ter o sentido oposto. O módulo da força magnética exercida sobre um segmento infinitesimal da barra de comprimento , situado a uma distância do fio, é
Integrando força acima para toda barra, temos:
Como o campo produzido pelo fio aponta para fora do papel na região onde a barra está se movendo e o sentido da corrente na barra é para cima, a força associada ao campo magnético aponta para a direita e, portanto, a força externa aplicada deve apontar para a esquerda.
E por fim, a taxa com a qual a força externa realiza trabalho sobre a espira é:
Como toda a energia fornecida pela força externa é convertida em energia térmica, este valor é igual ao da potência dissipada na espira, calculado no item c.
E aí! O que achou? Responde Aí! 😉
Resposta
a) ;
b) ;
c) ;
d) ;
e) .