Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.Problemas Adicionais - Ex. 79
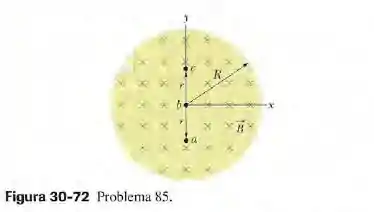
A figura 30-72 mostra um campo magnético uniforme confinado a um volume cilíndrico de raio . O módulo de está diminuindo a uma taxa constante de . Em termos dos vetores unitários, determine a aceleração inicial de um elétron liberado (a) no ponto (a uma distância do eixo do cilindro); (b) no ponto (); (c) no ponto (.
Passo 1
E aí, galerinha! 😁
Nesse problema temos um eletron que sofre a ação de um campo magnético e nosso objetivo é determinar a aceleração inicial do eletron no ponto , e .
Parece complicado? 🤔
O campo elétrico induzido é dado por:
Como, para a configuração da figura 30-72, as linahs de campo elétrico são circunferências concêntricas com o eixo do cilindro, temos, para uma trajetória ao longo de uma linha de campo elétrico:
Como a força que o campo exerce sobre um elétron é , a aceleração do elétron, de acordo com a segunda le ide Newton, é .
Tranquilo até aqui? 😉
Passo 2
No ponto ,
Considerando positivo o sentido da normal para dentro do papel, que é o sentido do campo magnético, o sentido positivo do campo é o sentido horário. Assim, o sentido do campo elétrico no ponto é para a esquerda, o que nos dá . A aceleração resultando é:
Passo 3
No ponto , nós temos o raio . Desse modo, o campo elétrico é igual a zero e, portanto, .
O campo elétrico no ponto tem o mesmo módulo que no ponto e o sentido oposto. Assim, a aceleração de um elétron liberado no ponto é
E aí! O que achou? Responde Aí! 😁
Resposta
a)
b) ;
c) .