Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.Problemas Adicionais - Ex. 97
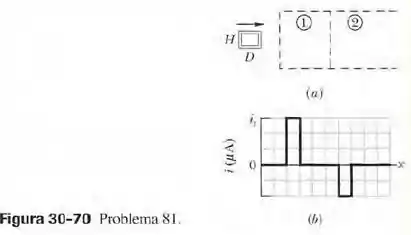
A figura 30-70a mostra uma espira retangular de resistência , altura e comprimento , que é puxada com velocidade escalar constante e passa por duas regiões onde existem campos magnéticos uniformes. A figura 30-70b mostra a corrente induzida na espira em função da posição do lado direito da espira. A escala do eixo vertical é definida por . Assim, por exemplo, uma corrente de no sentido horário é induzida quando a espira penetra na região 1. Determine (a) o módulo e (b) o sentido (para dentro ou para fora do papel) do campo magnético na região 1. Determine também (c) o módulo e (d) o sentido do campo magnético na região 2.
Passo 1
Bom, galera, o módulo da força eletromotriz induzida em uam espira condutora é igual à taxa de variação com o tempo do fluxo magnético que atravessa a espira. A expressão para caluclar a força eletromotriz é a seguinte:
O sinal negativo mostra que a força eletromotriz se opõe à variação do fluxo.
Aqui, podemos usar a lei de Ohm para relacionar a corrente induzida à fem, que é dada pela lei de Faraday:
Quando a espira penetrou parcialmente na região 1, de modo que uma parte do comprimento da espira está na região , o fluxo é:
o que significa que
Observando a figura 30-70b, vemos que, nessa situação, , o que nos dá
Assim, de acordo com a lei de Lens, o sentido do campo magnético na região 1 é para fora do papel.
Passo 2
Quando a espira penetrou parcialmente na região 2, de modo que uma parte do comprimento da espira está na região 2 e uma parte está na região 1, o fluxo é:
o que significa que
Observando a figura 30-70b, vemos que, nessa situação, , o que nos dá
Assim, de acordo com a lei de Lenz, o sentido do campo magnético na região 2 é para fora do papel.
Resposta
- ;
- O sentido do campo magnético na região 1 é para fora do papel;
- ;
- O sentido do campo magnético na região 2 é para fora do papel.