Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 33.Exercícios e Problemas - Ex. 22
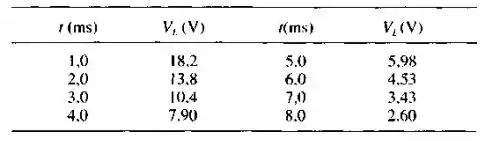
No instante , ligamos uma bateria em série com um indutor e um resistor. A tabela abaixo dá a diferença de potencial, em volts, através do indutor após a ligação da bateria. Determinar (a) a fem da bateria e (b) a constante de tempo do circuito.
Passo 1
Oii pessoal, show de bola??
“A loucura é como a gravidade, só precisa de um empurrãozinhooo...”
Bora empurrar e macetar essa questãozinha comigo agora
A equação que rege a tensão no indutor é
Onde o subíndice serve para indicar convenientemente o instante de tempo que queremos considerar.
Vamos usar dois pontos quaisquer da tabela que foi dada, como por exemplo , temos que
Ou seja
Passo 2
Portanto, trabalhando na expressão anterior
Substituindo os valores numéricos, teremos
Passo 3
Agora, para obter o valor de , basta usar o fato que , substituindo-se nesta formula qualquer um dos pontos da Tabela. Por exemplo, usando-se o primeiro ponto da Tabela obtemos:
Passo 4
Observe que na expressão acima usamos milissegundos como unidade de tempo, para abreviar os cálculos. E fácil conferir agora que a equação
permite obter-se corretamente qualquer um dos outros pontos na Tabela.
“Faça seus medos terem medo de você”
Resposta
Resposta nos passos.