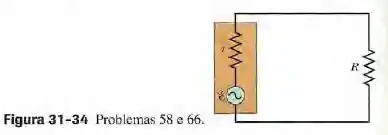
Na figura 31-34, suponha que o retângulo da esquerda representa a saída (de alta impedância) de um amplificador de áudio, com . Suponha que represente a bobina (de baixa impedância) de um alto-falante. Para que a transferência de energia para a carga sejá máxima, devemos ter , o que, neste caso, não é verdade. Entretanto, os transformadores podem ser usados para “transformar” resistências, fazendo com que se comportem eletricamente como se fossem maiores ou menores do que realmente são. (a) Modifique o circuito da figura 31-34 de modo a incluir um transformador a ser introduzido entre o amplificador e o alto-falante para casar as impedâncias. (b) Qual deve ser a relação de espiras?
Passo 1
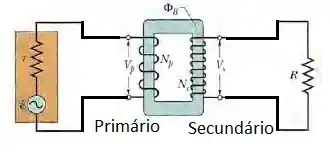
O amplificador deve ser ligado ao enrolamento primário de um transformador e o resistor deve ser ligado ao enrolamento secundário. O desenho está logo abaixo
Passo 2
Vamos chamar de é a corrente rms no enrolamento secundário, a potência média fornecida ao resistor é:
Como , temos:
Na qual é a corrente no enrolamento primário. O circuito primário é formado pelo gerador e duas resistências em série: a resistência de saída do amplificador, , e a resistência equivalente do enrolamente primário. Assim,
Substituindo na equação da potência:
Passo 3
A gente quer saber a relação de espiras nesse transformador que foi inserido no circuito, ou seja, queremos , para qual é máxima. Vamos chamar , temos:
Derivando a equação anterior e igualando o resultado a zero, temos:
O que nos dá:
Como é diretamente proporcional a para pequenos valores de e inversamente proporcional a para grandes valores de , o extremo correspondente a é realmente um máximo, e não um mínimo. Como , concluímos que a transferência de energia é máxima para
Resposta
- O desenho está no passo 1;
- .