Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 31.1 - Ex. 38

A Figura 31-57 mostra um feixe de luz incidente em uma

placa de vidro de espessura de indice de refracao n.(a)Determine o

angulo de incidencia para que a separacao b entre o raio refletido da

superficie de cima e o raio refletido da superficie de baixo que sai pela

Passo 1

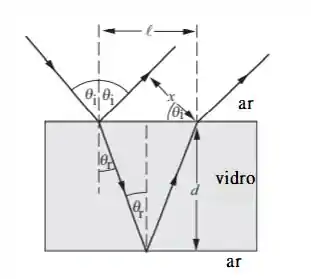
Seja x a separação perpendicular entre os dois raios e seja l   a separação entre os pontos de emergência dos dois raios na superfície do vidro. Podemos usar a geometria dos raios refratados e refletidos para expressar x como um função de l ,   d ,   θ r e θ i . Vamos definir a derivada da equação resultante igual a zero resultará no valor θ i , que maximiza x.

Passo 2

Letra a:

Expresse l em termos do ângulo de refração θ r

l = 2 d t a n ⁡ θ r

Expresse x como uma função de l ,   d ,   θ r e θ i

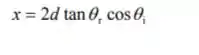
Diferencie x com respeito à θ i :

d x d θ 1 = 2 d d d θ 1 t a n ⁡ θ r c o s ⁡ θ 1 = 2 d - t a n ⁡ θ r s i n ⁡ θ 1 + s e c 2 ⁡ θ t c o s ⁡ θ i d θ r d θ 1                   ( 1 )

Aplique a lei de Snell à interface ar-vidro:

n 1 sin ⁡ θ 1 = n 2 sin ⁡ θ r                   ( 2 )   o u ,   c o m o   n 1 = 1   a n d   n 2 = n s i n ⁡ θ 1 = n s i n ⁡ θ r

Diferencie implicitamente em relação à θ i para obter:

c o s ⁡ θ 1 d θ 1 = n c o s ⁡ θ r d θ r   o u   d θ r d θ i = 1 n cos ⁡ θ 1 cos ⁡ θ r

Passo 3

Substitua na equação (1) para obter:

d x d θ 1 = 2 d - sin ⁡ θ t cos ⁡ θ r s i n ⁡ θ 1 + 1 n cos ⁡ θ i cos 2 ⁡ θ r cos ⁡ θ i cos ⁡ θ r = 2 d 1 n cos 2 ⁡ θ i cos 3 ⁡ θ r - s i n ⁡ θ r s i n ⁡ θ i cos ⁡ θ r

Substitua 1 - s i n 2 ⁡ θ 1  por   c o s 2 ⁡ θ i e 1 n s i n ⁡ θ i  por   s i n ⁡ θ t   para obter

d x d θ i = 2 d 1 - s i n 2 ⁡ θ i n c o s 3 ⁡ θ r - sin 2 ⁡ θ i n c o s ⁡ θ r

Multiplique o segundo termo entre parênteses por c o s 2 θ r / c o s 2 θ r e simplifique para obter:

d x d θ i = 2 d 1 - s i n 2 ⁡ θ i n c o s 3 ⁡ θ r - s i n 2 ⁡ θ i c o s 2 ⁡ θ r n c o s 3 ⁡ θ r = 2 d n c o s 3 ⁡ θ r 1 - s i n 2 ⁡ θ i - s i n 2 ⁡ θ 1 c o s 2 ⁡ θ r

Substitua 1 - s i n 2 ⁡ θ r  por   c o s 2 ⁡ θ r :

d x d θ i = 2 d n c o s 3 ⁡ i 1 - s i n 2 ⁡ θ i - s i n 2 ⁡ θ i 1 - s i n 2 ⁡ θ r

Substitua 1 n s i n ⁡ θ i  for  s i n ⁡ θ r para obter:

d x d θ i = 2 d n c o s 3 ⁡ θ r 1 - s i n 2 ⁡ θ i - s i n 2 ⁡ θ i 1 - 1 n 2 s i n 2 ⁡ θ i

d x d θ i = 2 d n 3 c o s 3 ⁡ θ r s i n 4 ⁡ θ i - 2 n 2 s i n 2 ⁡ θ i + n 2 = 0  para  extremo

Se d x / d θ i = 0 , então deve ser verdade que:

s i n 4 ⁡ θ i - 2 n 2 s i n 2 ⁡ θ i + n 2 = 0 θ i = s i n - 1 ⁡ n 1 - 1 - 1 n 2

Passo 4

Letra b:

Avalie θ i  para  n = 1.60

θ 1 = s i n - 1 ⁡ 1.6 1 - 1 - 1 ( 1.60 ) 2 = 48.5 ∘

Passo 5

Letra c:

Em (a), mostramos que:

x = 2 d t a n ⁡ θ r c o s ⁡ θ i

então,

θ r = s i n - 1 ⁡ n 1 n 2 sin ⁡ θ i θ r = s i n - 1 ⁡ 1 1.60 sin ⁡ 48.5 ∘ = 27.9 ∘ x = 2 ( 4.0 c m ) t a n ⁡ 27.9 ∘ c o s ⁡ 48.5 ∘ = 2.8 c m

Resposta

  1. θ i = sin - 1 ⁡ n 1 - 1 - 1 n 2
  2. 48.5 ∘
  3. = 2.8 c m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura mostra uma lâmpada pendurada a uma distância d 1 = 250c m acima da superfície da água de uma piscina na qual a profundidade da água é d 2 = 200c m . O fundo da piscina é um espelho. A que dis
Este problema e uma analogia a refracao.Uma banda estamarchando em um campo de futebol com uma velocidade constante。Aproximadamente na metade do campo,a banda entra em umasecao de lama que tem uma fro
Em um safari,voce esta com uma lanca em um rio,Voceobserva um peixe deslizando na sua direcao.Se sua linha de visadaate o peixe esta 64,0 abaixo da horizontal no ar e considerando quea lanca segue uma
Voce esta parado na borda de uma piscina e olhando di-retamente para o lado oposto.Voce nota que o fundo do lado opos-to da piscina parece estar a um angulo de 28 abaixo da horizontal.Entretanto,quand