Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.1 - Ex. 5
A figura mostra uma lâmpada pendurada a uma distância acima da superfície da água de uma piscina na qual a profundidade da água é . O fundo da piscina é um espelho. A que distância da superfície do espelho está a imagem da lâmpada? (Sugestão: suponham que os raios não se desviam muito de uma reta vertical passando pela lâmpada e use a aproximação, válida para pequenos ângulos de que )
Passo 1
Para começarmos a resolver o problema vamos esquematizalo a partir de um desenho:
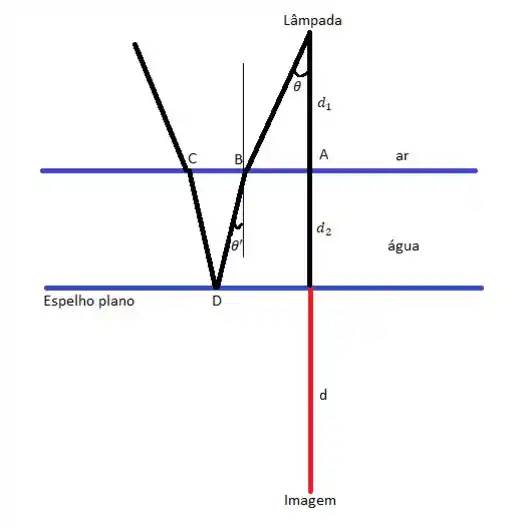
Nesse caso temos que a luz está sofrendo uma refração logo vamos precisar utilizar a lei de Snell:
Passo 2
Para esse problema podemos considerar que e , temos também que , desta forma a lei de Snell se reduz à:
Na figura conseguimos observar o triângulo formado pela lâmpada, o ponto A e o ponto B, que nos dá:
Mas , então:
Outro triângulo que conseguimos observar é o formado pelos pontos A,B e C, que nos dá:
Mas , então:
Por ultimo conseguimos verifocar o tirângulo formado pela imagem (I), o ponto A e C, que nos dá:
Passo 3
Nosso objetivo é encontrar e agora com todos esse dados podemos calcular ele a partir da relação:
Substituindo os valores (, e ):
Resposta
A distância da imagem até o espelho é .