Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 28.1 - Ex. 65

PLANILHA ELETRONICA Dado o circuito mostrado na Figura

28-55,considere que o indutor tenha resistencia interna desprezivel

e que a chave S tenha estado fechada por um longo tempo,existindo

uma corrente estacionaria no indutor.(a)Determine a corrente na bate-

ria,a corrente no resistor de 100e a corrente no indutor.(b)Determi-

ne a queda de potencial no indutor imediatamente depois de a chave

S ter sido aberta.(c)Usando uma planilha eletronica,faca graficos da

corrente no indutor e da queda de potencial no indutor como funcoes

do tempo,para o periodo durante o qual a chave esta aberta.

Passo 1

A fem auto-induzida no indutor é proporcional à taxa na qual a corrente que passa por ele está mudando. Sob condições de estado estacionário, d l / d f = 0 e, portanto, a fem auto-induzida no indutor é zero. Podemos usar a lei das tensões de Kirchhoff para obter a corrente e a tensão através do indutor em função do tempo.

Letra a:

Como, sob condições de estado estacionário, a fem auto-induzida no indutor é zero e como o indutor tem resistência desprezível, podemos aplicar a lei das tensões de Kirchhoff à malha que inclui a fonte, o resistor 10 Ω e o indutor 2 H para encontrar a corrente retirada da bateria e fluindo através do indutor e do resistor 10 Ω :

10 V - ( 10 Ω ) I 10 - Ω = 0

Resolvendo para I 10 Ω , temos:.

I 10 - Ω = I 2 - H = 1.0 A I 100 - Ω = I bateria  - I 2 - H = 0

Passo 2

Letra b:

Quando a chave é aberta, a corrente não pode ir imediatamente para zero no circuito por causa do indutor. Por um tempo, uma corrente circulará no circuito entre o indutor e o resistor 100 Ω . Como a corrente que flui através deste circuito é inicialmente 1 A , a queda de tensão no resistor 100 Ω é inicialmente 100 V .  

A conservação de energia (lei das tensões de Kirchhoff) requer que a queda de tensão no indutor 2 H   seja V 2 H = 100 V

Passo 3

Letra c:

Aplique a lei das tensões de Kirchhoff ao circuito RL para obter:

L d I d t + I R = 0

A solução para esta equação diferencial é:

I ( t ) = I 0 e - R L ' = I 0 e - 1 r   o n d e   τ = L R = 2.0 H 100 Ω = 0.020 s

Um programa de planilha para gerar os dados para gráficos da corrente e da tensão através do indutor como funções do tempo é mostrado abaixo. As fórmulas usadas para calcular as quantidades nas colunas são as seguintes:

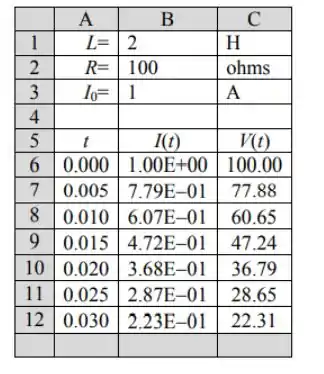
Passo 4

O gráfico a seguir da corrente no indutor em função do tempo foi traçado usando os dados nas colunas A e B do programa de planilha.

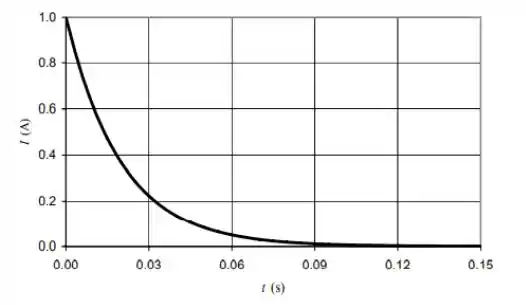
O gráfico a seguir da tensão através do indutor em função do tempo foi traçado usando os dados nas colunas A e C do programa de planilha

Resposta

  1. 1.0A e 0
  2. A conservação de energia (lei das tensões de Kirchhoff) requer que a queda de tensão no indutor 2 H   seja V 2 H = 100 V
  3. Ver resolução
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

42 . Um solenoide toroidal possui 2.900 espiras enroladas bem próximas, área de seção reta igual a 0,450c m 2 , raio médio de 9,00c m e resistência R = 2,80Ω . Ignore a variação do campo magnético pel
Num circuito LC, um indutor de 1.50 mH armazena uma energia máxima de 10,0 μ J. Qual é o pico de corrente?
O fluxo concatenado total através de uma certa bobina de 0.75 Ω de resistência vale 26 mW, quando e percorrida por uma corrente de 5.5 A. (a) Calcular a indutância da bobina. (b) Se uma bateria de 6 V
Suponha que a fem da bateria nu circuito da Fig. 33-6 varie com o tempo t de tal modo que a corrente seja dada por i ( t )=3,0+5,0 t , onde i é dado em amperes e t em segundos. Faça R=4,0 Ω ,L = 6.0H
Na Figura 33-17, E=100V ,R 1=10Ω ,R 2=20Ω ,R 3=30ΩeL=2H . Determine os valores de i 1ei 2 (a) imediatamente após o fechamento da chave S; (b) muito tempo depois do fechamento de S; (c) imediatamente a