Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 33.6 - Ex. 60

Na Fig. 33-58, a luz do raio A é refratada pelo meio 1 ( n 1   =   1,60 ), atravessa uma fina camada do meio 2 ( n 2   =   1,80 ) e incide com o ângulo crítico na interface dos meios 2 e 3 ( n 3 = 1,30 ).

(a) Qual é o valor do ângulo de incidência θ A ?

(b) Se θ A diminuir, parte da luz conseguirá passar para o meio 3?

A luz do raio B é refratada pelo material 1, atravessa o material 2 e incide com o ângulo crítico na interface dos materiais 2 e 3.

θ B ?

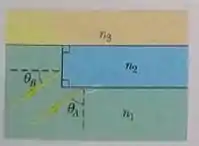
(d) Se θ B ? diminuir, parte da luz conseguirá passar para o meio 3?

.

Passo 1

Letra a)

Como o ângulo é crítico entre os meios 2 e 3 temos:

s e n θ c = n 3 n 2

E daí podemos calcular o ângulo θ A pela lei de Snell:

n 1 s e n θ A = n 2 s e n θ c

n 1 s e n θ A = n 2 . n 3 n 2 = n 3

s e n θ A = n 3 n 1 = 1,3 1,6

θ A = 54,34 °

Passo 2

Letra b)

Se θ A diminuir, então s e n θ A também diminui, e teremos ela lei de Snell:

s e n θ = n 1 n 2 s e n θ A

Daí o ângulo refratado θ vai ser menor do que o ângulo crítico, possibilitando a passagem do raio luminoso para o meio 3.

Passo 3

Letra c)

Agora o ângulo de refração é em relação à normal referente ao ângulo θ B . O ângulo crítico é o mesmo determinado no passo 1 , θ c = 46,23 ° , mas agora esse ângulo deve estar em relação à normal da outra interface, ou seja, 90 - 46,23 = 43,77 ° .

Aplicando a le de Snell para determinar o valor de θ B temos:

n 1 s e n θ B = n 2 s e n θ c

s e n θ B = 1,8 s e n 43,77 1,6 = 0,77

θ B = 51,1 °

Passo 4

Letra d)

Aqui o raciocínio é pouco diferente. Se θ B diminuir, o ângulo crítico vai aumentar agora, e como para qualquer ângulo acima do ângulo crítico não há refração, não tem como o raio luminoso passar para o meio 3.

Resposta

a ) θ A = 54,34 °

b ) s i m

c ) 51,1 °

d ) n ã o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um raio de luz está se propagando em um cubo de vidro que está completamente imerso na água. Você descobre que, se o raio incide sobre a interface vidro-água em um ângulo maior do que 48 , 7 ° com a n
A luz incide na direção da normal na face A B de um prisma de vidro de índice de refração 1,52 , como mostra a Figura 33.41. Encontre o maior valor que o ângulo α pode ter para que nenhu- ma luz seja
Um prisma de ângulos 45 ° -45 ° - 90 ° está imerso na água. Um raio de luz incide perpendicularmente sobre uma de suas faces menores. Qual é menor indice de refração que o prisma deve ter para que o r
As placas fotográficas antigas eram feitas de vidro com uma emulsão sensível à luz sobre a superfície frontal. Essa emulsão era ligeiramente transparente. Quando uma fonte puntiforme brilhante é focal
Um grande cubo de vidro possui um refletor de metal em uma das faces e água na face adjacente (Figura 33.52). Um feixe de luz incide sobre o refletor, como mostrado na figura. Você observa que, à medi