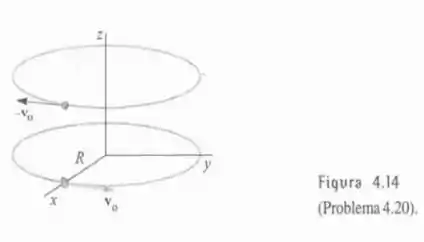
A figura 4.14 mostra duas bolinhas realizando movimento circular uniforme em sentidos opostos, sobre círculos de mesmo raio deslocados um do outro na direção vertical. Tomando como tempo t=0 aquele do instantâneo mostrado na figura, calcule:
A) A velocidade.
B) A aceleração da bolinha ocre relativamente à bolinha azul.
Passo 1
Meus dengos!
a)
Sabemos que a fórmula da velocidade circular em função do tempo é dada por:
Sabemos que a seguinte relação é válida:
OBS:
Como queremos a velocidade relativa:
Passo 2
b)
Agora vamos fazer a letra b!
Sabemos que:
Para saber a aceleração relativa: