Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 44
Figura abaixo, e o coeficiente de atrito estático entre o bloco e o plano inclinado é , (a) Encontre a faixa de valores possíveis para para a qual o sistema permanecerá em equilíbrio estático. (b) Encontre a força de atrito sobre o bloco de se .
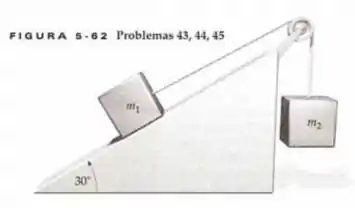
Passo 1
a) Olá, tá bem?
Então, vamos refletir. Temos um bloco na rampa e ele está ligado a outro bloco que está pendurado. Só o sistema está em equilíbrio, ou seja, está todo mundo paradinho.
Mas não sabemos , então a gente não sabe se ela é maior que e o bloco pendurado puxaria o outro para direita. Ou se é maior e esse bloco tende a deslizar para esquerda, puxando a massa .
E é exatamente isso que o enunciado pede. Ele quer saber o intervalo de valores que pode ter para que esse sistema fique em equilíbrio.
Vamos fazer um diagrama de corpo livre da situação:
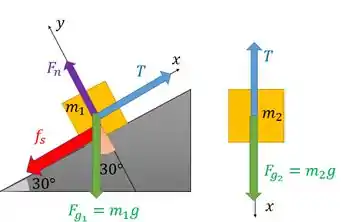
Percebe que a gente colocou nos dois blocos a força peso para baixo. A tensão onde temos a corda. porque há contato entre o bloco e a superfície. E colocamos a força de atrito estático .
Mas percebe que essa força precisa estar no sentido contrário à tendência do movimento. Só que a gente não sabe o sentido dessa tendência porque não sabe . Então representamos ali para um sentido, mas nas equações a gente vai considerar que ela pode estar no outro sentido também, ok?
Ah e atenção ao nosso sistema de coordenadas. É legal colocar na direção do movimento. Mas cê pode escolher outros sistemas.
Bora!
Passo 2
De acordo com a 2° Lei de Newton no eixo x para o bloco , vamos ter
Como estamos em equilíbrio, , então:
Aí nessa direção, a gente tem positiva (no sentido positivo de ), temos , mas ela pode estar em um sentido positivo ou negativo, então vamos colocar no somatório. E temos também a componente de que é dada por que aponta para negativo.
O somatório de forças fica
Agora a segunda lei de Newton para esse mesmo bloco para a direção , sabendo que :
Nessa direção temos a força normal para a parte positiva e a componente de para baixo. O somatório fica:
Passo 3
Então a gente tem essas duas equações:
Aí a gente pode lembrar que a força de atrito estático máxima é dada por:
Substituindo a expressão de de
E substituindo essa expressão de em :
Passo 4
Usando a 2° Lei de Newton para o bloco 2 em x, temos:
Somando essa equação com a última equação do passo 3, temos:
Substituindo os valores numéricos:
Aí temos dois valores de , um se a gente usar o sinal de menos e outro se a gente usar o sinal de mais:
ou
Esses dois valores encontrados são os limites possíveis para a massa para o sistema permanecer em equilíbrio. Portanto,
Passo 5
b) Queremos o valor da força de atrito agora para que haja equilíbrio.
Com , a tendência de movimento do bloco 1 é para esquerda, já que o bloco de vai ter maior massa. Portanto, nesse caso, a força de atrito tem o mesmo sentido da tração no bloco 1. Assim:
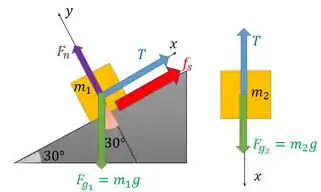
A segunda lei de Newton na direção para o bloco fica
Repara fica positiva porque sabemos seu sentido. Para o bloco o somatório em fica:
Somando essas duas equações:
Substituindo por valores numéricos: