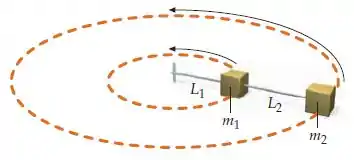
Um bloco de massa m 1 está preso a uma corda de comprimento L 1 , que está fixada por uma de suas pontas. O bloco se move em um círculo horizontal em um tampo de mesa sem atrito. Um segundo bloco de massa m 2 está preso ao primeiro por uma corda de comprimento L 2 e também se move em um círculo no mesmo tampo, como mostrado na figura. Se o período do movimento é T , encontre a tensão em cada corda em termos das variáveis que foram dadas.

Na corda de comprimento L 1 , a tensão é T 1 = 4 π 2 T 2 L 1 m 1 + L 1 + L 2 m 2 . Na corda de comprimento L 2 , a tensão é T 2 = L 1 + L 2 4 π 2 m 2 T 2 .

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 81

Um bloco de massa está preso a uma corda de comprimento , que está fixada por uma de suas pontas. O bloco se move em um círculo horizontal em um tampo de mesa sem atrito. Um segundo bloco de massa está preso ao primeiro por uma corda de comprimento e também se move em um círculo no mesmo tampo, como mostrado na figura. Se o período do movimento é , encontre a tensão em cada corda em termos das variáveis que foram dadas.

Passo 1

Vamos fazer um desenho com a vista de cima do sistema:

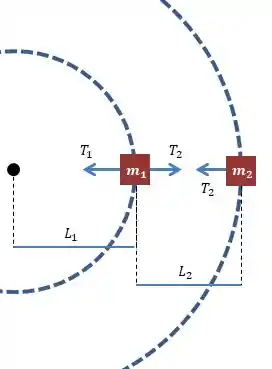
Para manter o movimento circular, cada um dos blocos precisa ter uma resultante centrípeta compatível com certo raio e um período :

Então vamos aplicar essa equação a cada um dos blocos.

Passo 2

Começando pela massa , para a qual , então:

E para a massa :

A expressão para já está pronta, só precisamos substituí-la na equação de cima para encontrar :

Pronto, agora tudo está em termos das variáveis dadas no enunciado.

Resposta

Na corda de comprimento , a tensão é . Na corda de comprimento , a tensão é .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Um bloco está deslizando para baixo em um plano inclinado. O coeficiente de atrito cinético entre o bloco e o plano é μ k . Mostre que o gráfico de a x / cos ⁡ θ em função de tan ⁡ θ (onde a x é a

Um bloco de 10,0k g está em repouso sobre um suporte de 5,0k g , como mostrado na figura. O suporte de 5,0k g está sobre uma superfície sem atrito. Os coeficientes de atrito entre o bloco de 10,0k g e

Um bloco de 100 kg em um plano inclinado está preso a outro bloco de massa m através de uma corda, como nas figuras. Os coeficientes de atrito estático e cinético para o bloco e o plano inclinado são

Para determinar o coeficiente de atrito cinético de um bloco de madeira sobre a superfície horizontal de uma mesa, a seguinte tarefa é dada a você: pegue o bloco de madeira e dê-lhe uma velocidade ini

Uma barra rígida com uma bola de 0,050k g em uma das suas extremidades roda em torno da outra extremidade de forma que a bola viaje com rapidez constante em um círculo vertical de raio r = 0,20m . Qua