Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 80
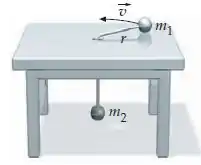
Um pequeno objeto de massa se move por um caminho circular de raio em um tampo de mesa horizontal sem atrito. Ele está preso a uma corda que passa por um buraco pequeno e sem atrito no centro da mesa. Um segundo objeto com uma massa está preso na outra ponta da corda. Deduza uma expressão para em termos de , e o tempo de uma revolução.
Passo 1
Cara, vamos lá! Temos um movimento circular sobre a mesa sem atrito. Isso quer dizer que essa bolinha está andando em uma trajetória circular. E para que ela faça isso, é necessário que haja uma força atuando nela apontando para o centro do círculo.
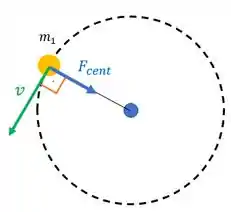
Essa força é chamada de força centrípeta! E ela tem essa equação:
Onde é a massa da bolinha, é a velocidade dela e é o raio do círculo que é a trajetória dessa bolinha.
Só que essa força centrípeta precisa de fato existir na situação. Ou seja, alguém precisa aplicar uma força na bolinha e fazer esse papel de força centrípeta. Aí a gente pensa: que força na nossa situação aponta para o centro do círculo?
A tensão na cordinha! Certo? Essa cordinha que prende a bolinha na massa . Então podemos escrever
Substituindo nossa expressão para :
Como queremos achar :
Só não temos a velocidade da bolinha e a tensão na corda ainda. Vamos achar essas coisinhas!
Passo 2
A tensão na corda é a mesma para todos os pontos. Se a gente olhar para a massa e fizer o diagrama de corpo livre dela, vamos ter:
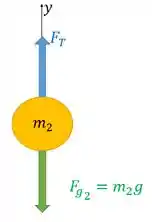
Aplicando a segunda lei de Newton nesse carinha:
Essa bolinha está parada, então :
Substituindo isso na nossa expressão de :
Passo 3
Agora precisamos achar alguma forma de reescrever , vamos tentar pela própria definição da velocidade média:
Como estamos tratando de um movimento circular o comprimento circulo vai ser a distância percorrida:
E tempo decorrido em uma volta é (período) que é o tempo de uma revolução
Assim a velocidade fica:
Passo 4
Substituindo isso na equação do passo 2
Cortando dos dois lados e isolando mais uma vez:
Resposta
A expressão é .