Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.5 - Ex. 43

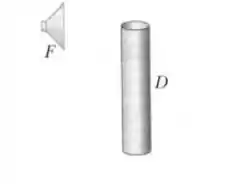
Na figura abaixo, F é um alto-falante alimentado por um oscilador de áudio com uma frequência que varia entre 1000 H z a 2000 H z e D é um tubo cilíndrico com 45,7 c m de comprimento e as duas extremidades abertas. A velocidade do som no ar do interior do tubo é 344 m / s . ( a ) Para quantas frequências o som do alto-falante produz ressonância no tubo? Qual é ( b ) a menor e ( c ) a segunda menor frequência de ressonância?

Passo 1

Considerando um tubo com as duas extremidades abertas, sabemos que as frequências de ressoâncias f n se relacionam com o harmônico n da seguinte forma:

f n = 2 n 4 v L

E como sabemos a velocidade do som no tubo, vamos determinar a relação entre f n e n :

f n = 2 n 4 344 0,457 = 376,36 n

f n = 376,36 n

Passo 2

Sabendo da relação entre f n e n , e sabendo também o intervalo de frequências emitido pelo alto-falantes, podemos determinar quantas frequências de ressonância:

  • Para n = 1 : f 1 = 376,36 H z → está fora do intervalo de frequência
  • Para n = 2 : f 2 = 752,73 H z → está fora do intervalo de frequência
  • Para n = 3 : f 3 = 1129,10 H z → está dentro do intervalo de frequência
  • Para n = 4 : f 4 = 1505,47 H z → está dentro do intervalo de frequência
  • Para n = 5 : f 5 = 1881,83 H z → está dentro do intervalo de frequência
  • Para n = 6 : f 6 = 2258,20 H z → está fora novamente do intervalo de frequência

Então, dentro do intervalo (que está entre 1000 H z a 2000 H z ) são admitidas 3 frequências que satisfazem a condição de ressonância.

Passo 3

Já que sabemos as frequências de ressonância do passo anterior, podemos ver que a menor frequência é com n = 3 , ou seja f 3 = 1129,10 H z

Passo 4

Sendo assim, a segunda menor é com o próximo n inteiro: n = 4 , ou seja f 4 = 1505,47 H z .

Resposta

a 3   f r e q u ê n c i a s

b 1129,10 H z

c 1505,47 H z

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quatro ondas sonoras são produzidas no mesmo tubo cheio de ar, no mesmo sentido: s 1 x , t = ( 9 n m ) c o s ⁡ ( 2 π x - 700 π t ) s 2 x , t = ( 9 n m ) c o s ⁡ ( 2 π x - 700 π t + 0,7 π ) s 3 x , t =
Um tubo de 0,60 m de comprimento, fechado em uma extremidade, está cheio de gás desconhecido. A frequência do terceiro harmônico do tubo é 750 H z . a Qual é a velocidade do som no gás desconhecido? (
O cano A é aberto em apenas uma das extremidades; o tubo B é quatro vezes mais comprido e é aberto nas duas extremidades. Dos 10 menores números harmônicos n B do tubo B , qual é a o menor, ( b ) o se
A figura mostra um insterferômetro acústico, usado para demonstrar a interferência de ondas sonoras. A fonte sonora F é um diafragma oscilante. D é um detector de ondas sonoras, como o ouvido ou um mi