Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 18.3 - Ex. 21
Como resultado de um aumento de temperatura de , uma barra com rachadura no centro dobra pra cima . Se a distância fixa é e o coeficiente de dilatação linear da barra é , determine a altura do centro da barra.
Passo 1
Show de bolinhas pessoal tudo bem com vocês?
O enunciado nos deu que uma barra com uma rachadura no centro dobra pra cima devido ao aumento de temperatura de . Entao sabendo que a distância fixa é de e o coeficiente de dilatação linear da barra é , o enunciado nos pede para determinar a altura do centro da barra.
Aprincípio essa questão pode parecer ser um pouquinho difícil, mas vamos olhar o desenho com carinho:
Como a barra dilata linermente e a altura está no centro, podemos identificar um triângulo com as seguintes dimensões:
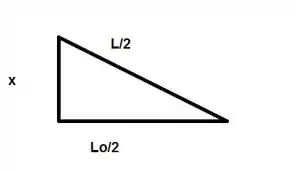
Sendo assim, aplicando Pitágoras, obtemos que:
Onde é a medida fixa fornecida no problema, é o comprimento final da barra e é a medida desejada. Agora bora lá ver como que vai ficar essa brincadeira.
Passo 2
Vamos manipular um pouco essa equação.
Substituindo a fórmula da expansão linear no Pitágoras que acabamos de determinar, temos:
Podemos substituir os valores de direto aqui e determinar . Mas como a gente é malandro, podemos simplificar as coisas um pouquinho, logo:
Colocando o em evidência:
Substituindo os valores dados pelo problema:
Portanto:
