Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.Problemas Adicionais - Ex. 93
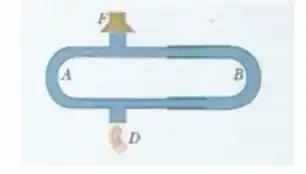
A figura mostra um insterferômetro acústico, usado para demonstrar a interferência de ondas sonoras. A fonte sonora é um diafragma oscilante. é um detector de ondas sonoras, como o ouvido ou um microfone; o tubo contém ar. O comprimento do tubo é fixo. Em , a onda sonora que se propaga no tubo interfere com a que se propaga no tubo . Em um experimento, a intensidade sonora do detector possui um valor de unidades para uma certa posição de e cresce , de maneira contínua, até um valor de unidades quando é deslocado . Determine a frequência do som emitido pela fonte e a razão entre as amplitudes no ponto da onda e da onda . Como é possível que as ondas tenham amplitudes diferentes, já que foram geradas pela mesma fonte?
Passo 1
Sabemos que a condição para ter interferência construtiva é que seja um múltiplo inteiro do meio comprimento de onda. Assim, como a diferença de caminho aumentou em duas vezes o percurso, temos:
Daqui temos a frequência emitida pela fonte:
Passo 2
Para determinar as intensidades nos dois pontos, temos :
E sendo a intensidade máxima e a intensidade mínima, temos que a razão entre é dado por:
Podemos portanto determinar a razão entre :
Passo 3
É possível pois o atrito que existe entre o ar e o tubo acaba reduzindo a energia das ondas durante o caminho percorrido. Como há dois caminhos diferentes, as ondas que se encontram em sofrem diferentes dissipações, ocasionando diferentes amplitudes.