Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 11.4 - Ex. 8
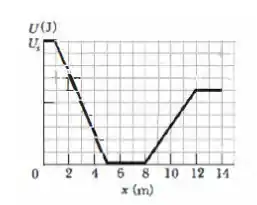
A figura abaixo mostra a energia potencial de uma bola maciça que pode rolar ao longo de um eixo . A escala do eixo é definida por . A bola é homogênea, rola suavemente e possui uma massa . Ela é liberada em quando se move no sentido negativo do eixo com uma energia mecânica de .
Se a bola pode chegar ao ponto qual é sua velocidade nesse ponto, e se não pode, qual é o ponto de retorno?
Suponha que a bola esteja movendo no sentido positivo do eixo ao ser liberada em com . Se a bola pode chegar ao ponto , qual é sua velocidade nesse ponto e se não pode, qual é o ponto de retorno?
Passo 1
Olá pessoal, tudo bem? Vamos praticar um pouco de energia rotacional? Dá uma olhadina no desenho que fiz em cima dessa figura do enunciado:
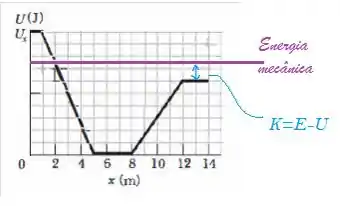
O ponto de reversão é aquele no qual a partícula já converteu toda sua energia mecânica em energia potencial e, pelo prinecípio de conservação, é máximo de troca de energia que ela pode realiza. Sendo assim, como a partícula foi lançada de e se desloca para a esquerda, o maior valor de energia potencial que ela pode atingir é a energia mecânica e isso acontece na posição . É onde a curva preta (energia potencial) encontra a curva roxa (energia mecânica- que é sempre constante em )
Passo 2
Agora vamos olhar pro lado direito daquela mesma figura do passo . Agora na posição a bola não só consegue chegar mas também tem velocidade diferente de zero.
Pelo princípio de conservação de energia temos que a soma das energias envolvidas vai ter o mesmo valor em qualquer ponto. Se a energia mecânica é e em a energia potencial gravitacional é (dá uma espiada na parte azul que desenhei), então a energia cinética vai ter um valor de .
Passo 3
A energia cinética agora vai ser dividida em energia cinética de rotação e de translação.
Como não há deslizamento a velocidade do centro de massa e o momento de inércia de uma bola maciça é . Bom, agora vamos substituir os valores:
Agora podemos juntar em uma só fração no lado esquerdo! Saca só:
Beleza! Agora é só tirar a raiz quadrada!
Show!
Bora treinar mais?