Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 9.Exercícios e Problemas - Ex. 11

9.11P Qual deve ser a massa da tábua no balanço da figura 9.19 para que o sistema fique em equilíbrio?

Passo 1

Belezoca galerinha, a figura mostrada pra gente é:

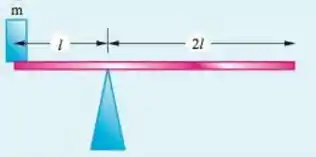
E para o sistema estar em equilíbrio, o somatório dos torques e das forças devem ser nulas:

∑       τ i = 0 ;     ∑       F i = 0

Mas nesse caso podemos olhar apenas para o torque, de forma que temos o torque exercido pelo bloco de massa m , mas também temos os torques exercidos pela força peso de cada parte da tábua de acordo com a divisão no eixo.

Passo 2

Então saca só, vamos supor que a massa total da tábua seja M , de forma que sua densidade linear seja:

ρ = M l + 2 l

ρ = M 3 l

Show de bola, então a massa M 1 da tábua do lado esquerdo do desenho cuja distância ao eixo é l , pode ser escrita como:

M 1 = ρ l

M 1 = M l 3 l = M 3

Já a segunda parte da tábua, do lado direito, está uma distância do eixo 2 l , tal que sua massa M 2 é dada por:

M 2 = ρ 2 l

M 2 = 2 M 3

Passo 3

Iradoso, então o torque do lado esquerdo, é dado pela força peso do bloco m e da força peso da tábua, só que o detalhe é que o bloco está à uma distância l do eixo, enquanto o centro de massa da parte esquerda da tábua está à uma distância l 2 , logo:

τ 1 = m g l + M 1 g l 2

τ 1 = m g l + M 3 g l 2

τ 1 = g l m + M 6

Já o torque do outro lado do sistema, é dado apenas pela força peso da parte direita da tábua, que está à uma distância 2 l 2 do eixo, logo:

τ 2 = M 2 g 2 l 2

τ 2 = 2 M 3 g l

Portanto, igualando os torques, temos que:

g l m + M 6 = 2 M 3 g l

m + M 6 = 2 M 3

m = 2 M 3 - M 6

m = M 3

Logo a massa total da tábua para que o sistema esteja em equilíbrio é:

M = 3 m

Resposta

M = 3 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma demonstração comum em sala de aula consiste em tomar uma régua de madeira de um metro e segurá-la horizontalmente, pela extremidade de 0,0c m , com uma quantidade de moedas de um centavo igualment
Uma barra fina uniforme de 0,25 k g , de 80 c m de comprimento, pode girar livremente em torno de um eixo fixo horizontal que passa, perpendicularmente, por uma de suas extremidades. Ela é largada da
Um disco uniforme de 120 k g , com raio igual a 1,4 m , gira inicialmente com uma rapidez angular de 1100 r e v / m i n . Uma força tangencial constante é aplicada a uma distância radial de 0,60 m do
No sistema descrito no problema 120, as constantes de força valem 60 N / m . O sistema parte do repouso e acelera lentamente até que as massas estejam a 0,80 m do centro do cilindro. Qual foi o trabal
A figura mostra um cilindro maciço de massa M e raio R , ao qual foi preso um segundo cilindro maciço, de massa m e raio r . Um cordão é enrolado em torno do cilindro menor. O cilindro maior está sobr