Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.4 - Ex. 10

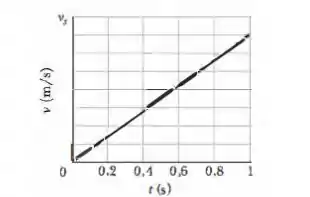
A figura abaixo mostra a velocidade escalar v em função do tempo t para um objeto de 0,5 k g e 6 c m de raio que rola suavemente para baixo em uma rampa de 30 ° . A escala do eixo das velocidades é definida por v s = 4 m / s . Qual é o momento de inércia do objeto?

Passo 1

Olá pessoal, tudo bem? Vamos praticar um pouco de dinâmica de rotação?

Essa fórmula aqui vai salvar a vida de vcs! Ela é aceleração do centro de massa do rolamento em função do momento de inércia:

a = - g s e n θ 1 + I c m / m r 2

Essa aqui tem que estar na ponta da língua! (ou melhor, do lápis =D)

Sabemos que a massa é m = 0,5 k g o raio do objeto é r = 0,06 m e que s e n 30 ° = 0,5 . Mas agora e a aceleração??

Passo 2

Ah! Dá uma espiada no gráfico ali em cima:

Não é um gráfico de velocidade em função do tempo?? Siiimm! Então é dali que pegaremos o valor da aceleração:

a = Δ v Δ t = 3,5 - 0 1 - 0 = 3,5 m / s ²

AQUI CUIDADO COM A ESCALA! O gráfico quaaaase nos induz que a velocidade varia de zero até 4 , mas não é! Ela vai só até 1 quadradinho antes do 4 . Como a escala é 4 e tem oito divisões, cada uma vale 0,5 de acréscimo na velocidade!

MAIS UMA COISA! O objeto se move no sentido negativo do x (olhem lá na seção do livro que deduz a fórmula que usei ali em cima), então a tem valor negativo!

Passo 3

Pronto! Agora é só isolar o I c m que é pedido:

a = - g s e n θ 1 + I c m / m r 2

a 1 + I c m m r 2 = - g s e n ( θ )

I c m m r 2 = - g s e n θ a - 1

I c m = m r 2 - g s e n θ a - 1

I c m = 0,5 . 0,06 2 - 9,8.0,5 - 3,5 - 1 = 7,2.10 - 4 k g m ²

Show!

Bora treinar mais?

Resposta

7,2.10 - 4 k g m ²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cilindro maciço e uniforme, de madeira, rola descendo um plano inclinado de um ângulo θ , sem deslizar. O coeficiente de atrito estático é μ . Determine (a) a aceleração do centro de massa do cilin
Uma esfera maciça e uniforme rola descendo um plano inclinado, sem deslizar. Se a aceleração linear do centro de massa da esfera é 0,20 g , qual é o ângulo de inclinação do plano com a horizontal?
Uma bola de basquete rola descendo um plano inclinado de um ângulo θ , sem deslizar. O coeficiente de atrito estático é μ . Trate a bola como uma casca esférica fina. Determine (a) a aceleração do cen
Um cilindro maciço e uniforme, de massa M e raio R , é colocado sobre uma barra de massa m , que, por sua vez, está sobre uma mesa horizontal sem atrito (figura 9-65). Se uma força F → é aplicada sobr
Uma bola de bilhar, inicialmente em repouso, recebe uma forte tacada. A força é horizontal e aplicada a uma distância 2 R 3 abaixo da linha diametral, como mostra a figura. A rapidez da bola imediatam