Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 34.Problemas - Ex. 101
Uma placa de vidro com espessura de e índice de refração é mantida com suas faces na horizontal, de modo que sua face inferior esteja acima de uma página impressa. Determine a posição da imagem formada pelos raios que fazem um pequeno ângulo com a normal ao plano.
Passo 1
Vamos começar fazendo um desenho da situação:
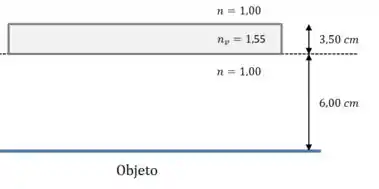
Já que estamos passando de um meio para o outro, vamos usar essa fórmula aqui:
Mas como a superfície é plana dos dois lados, o seu raio de curvatura tende ao infinito:
E a imagem final vai se formar depois de duas etapas: primeiro quando a luz passa do ar para o vidro (vindo de baixo), e depois quando passa do vidro de volta pro ar.
Passo 2
Começando pelo caso em que vamos do ar para o vidro ),
Pelo desenho, dá pra ver que a nossa fórmula vai ficar assim:
Ou seja, a primeira imagem se forma abaixo da parte de baixo do vidro:
Passo 3
Agora, essa imagem vai ser o objeto da nossa segunda refração.
Dessa vez, a distância do “objeto” até o vidro é:
E estamos indo do vidro ) para o ar (), então a fórmula fica:
E o sinal continua negativo. Isso quer dizer que a imagem final se forma abaixo da superfície de cima do vidro:
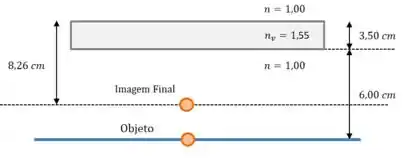
Isso quer dizer que a imagem final está acima da página.
Resposta
A imagem final é formada acima da página impressa.