Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 12.5 - Ex. 31
Na figura, uma barra não homogênea está suspensa em repouso, na horizontal, por duas cordas de massa desprezível. Uma corda faz um ângulo com a vertical; a outra faz um ângulo com a vertical. Se o comprimento da barra é , calcule a distância entre a extremidade esquerda da barra e o centro de massa .
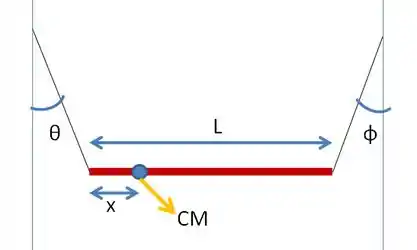
Passo 1
Fazendo um esquema de todas as forças que atuam sobre a barra, a gente consegue escrever as equações que demonstram o equilíbrio de forças na vertical e do equilíbrio de torques com relação ao centro de massa.
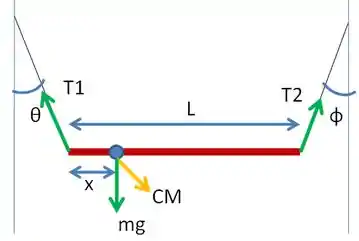
Isso é interessante pois com essas equações poderemos encontrar uma relação com a distância que queremos encontrar!
Do equilíbrio de torques com relação à extremidade esquerda da barra:
Do equilíbrio de forças na vertical:
Do equilíbrio de forças na horizontal:
Passo 2
Da terceira equação encontrada no passo 1, temos:
Substituindo esse valor de na equação do equilíbrio de forças na vertical, temos:
E se a gente colocar o em evidência vamos ter o seguinte:
Vamos substituir os valores pra gente não carregar essa sopa de letrinhas!
Passo 3
Agora, vamos usar a primeira equação do passo 1:
Substituindo o valor de nessa equação, a gente encontra a nossa resposta (valor de ):