Você é um engenheiro civil trabalhando no projeto interior de uma loja em um shopping center. Uma barra uniforme com 2,00 m de extensão e massa de 8,50 kg deve ser presa à parede em uma extremidade, por meio de uma dobradiça que permite que a barra gire livremente com muito pouco atrito. A barra será mantida em uma posição horizontal por um cabo leve a partir de um ponto na barra (uma distância x da dobradiça) até um ponto na parede acima da dobradiça. O cabo forma um ângulo u com a barra. O arquiteto propôs quatro formas possíveis de conectar o cabo e lhe pediu para avaliá-las:
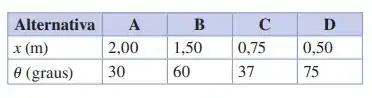
(a) Há uma preocupação sobre a resistência do cabo que será exigido. Qual conjunto de valores de x e u na tabela produz a menor tensão no cabo? E a maior? (b) Existe preocupação em relação à força de ruptura da parede de reboco, onde a dobradiça será presa. Qual é o conjunto de valores de x e u que produz o menor componente horizontal de força que a barra exerce sobre a dobradiça? E o maior? (c) Também há preocupação a respeito da resistência exigida da dobradiça e a resistência de sua conexão com a parede. Qual é o conjunto de valores de x e u que produz o menor módulo do componente vertical da força que a barra exerce sobre a dobradiça? E o maior? (Dica: a direção do componente vertical da força que a dobradiça exerce sobre a barra depende de onde o cabo está preso ao longo da barra.) (d) Existe alguma alternativa dada na tabela preferível às outras? Alguma das alternativas deverá ser evitada? Discuta.
Passo 1
E aii galera, vamos fazer mais uma questão?
Letra a:
Abaixo, o diagrama de corpo livre em equilíbro estático.
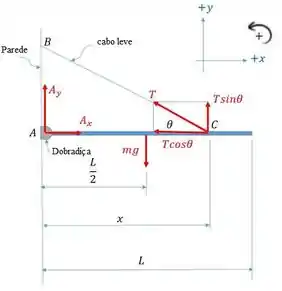
Temos:
E
Passo 2
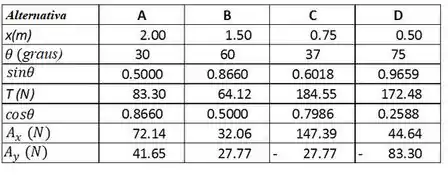
Em seguida nós fazemos a seguinte tabela baseada nos dados oferecidos:
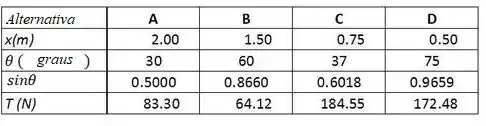
E calculamos:
T é a força do cabo na barra. Pela terceira Lei de Newton a tensão da barra no cabo tem direção oposta e a mesma magnitude. Então, o cabo está em tensão.
Passo 3
Letra b:
A força do componente horizontal que a barra exerce sobre a dobradiça é igual em magnitude e oposta em direção à força do componente horizontal que a dobradiça exerce sobre a barra .
Temos então:
Em seguida nós fazemos a seguinte tabela baseada nos dados oferecidos:
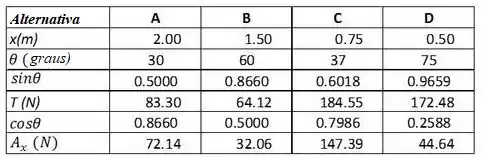
Passo 4
Letra c:
O componente vertical da força que a dobradiça exerce sobre a barra , tem a mesma magnitude, mas direção oposta da força do componente vertical exercida pela barra na dobradiça.
Temos então:
Em seguida nós fazemos a seguinte tabela baseada nos dados oferecidos:
Passo 5
Letra d:
Temos ainda a seguinte tabela:
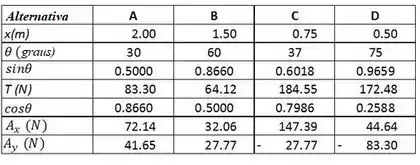
A alternativa B deve ser preferível, pois tem os valores menores para .
As alternativas C devem ser evitadas uma vez que tem os maiores valores para
Se a resistência da dobradiça e sua fixação à parede for uma preocupação crítica, a alternativa D deveria ser evitada.
Normalmente, quanto maior a magnitude das forças significa a necessidade de materiais mais caros. Mas a segurança é muito importante também. Portanto, de acordo com as forças encontradas, devemos selecionar materiais para o cabo, a dobradiça e a parede que pode ser capaz de suportar as forças que atuam sobre eles.
Resposta
Ver resolução