Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 11.3 - Ex. 17
Uma viga uniforme com 9,00 m de comprimento é articulada em uma parede vertical e mantida horizontalmente por um cabo de 5,00 m de comprimento preso à parede 4,00 m acima da dobradiça (Figura E11.17). O metal desse cabo possui uma resistência de teste de 1,00 kN, o que significa que ele se romperá se a tensão nele exceder essa quantidade. (a) Desenhe um diagrama do corpo livre da viga. (b) Qual é a viga mais pesada que o cabo poderá suportar nessa configuração? (c) Ache os componentes horizontal e vertical da força que a dobradiça exerce sobre a viga. O componente vertical é de baixo para cima ou de cima para baixo?
Passo 1
E aiiiiiiiii galera, tudo bom com vocês?
Vamos fazer mais uma questão!!
Letra a:
Uma vez que o feixe é uniforme, seu centro de gravidade encontra-se em seu centro geométrico. Abaixo, temos o diagrama de corpo livre:
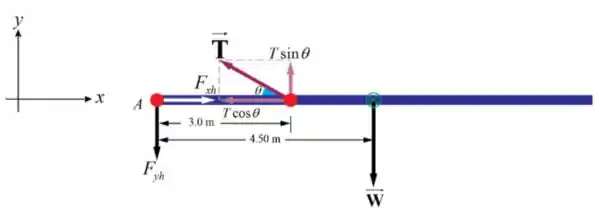
Passo 2
Letra b:
O ângulo feito pelo cabo com a viga é encontrado a partir da geometria da figura fornecida:
Deixe que as rotações no sentido anti-horário sejam positivas. Aplique a segunda condição para equilíbrio rotacional para a viga em torno de um eixo através da dobradiça:
onde 3,0 m é o braço de momento (encontrado do teorema de Pitágoras) e 4,50 m é o braço de momento de . A tensão máxima suportada pelo cabo corresponde ao peso máximo da viga. Então:
Passo 3
Letra c:
Deixe que o sentido para cima e para a direita sejam positivos. Aplique a primeira condição para o equilíbrio translacional para a viga na direção vertical:
Use o caso limite onde a tensão e o peso são máximos:
O componente vertical da força da dobradiça é direcionado para baixo.
Aplique a primeira condição para equilíbrio translacional para o feixe na direção horizontal:
Resposta
- é a tensão no cabo, é o componente vertical da força exercido pela dobradiça, é o componente horizontal da força exercida pela dobradiça, W é o peso gravitacional do feixe.