Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 11.Problemas - Ex. 59
Como parte de um programa de exercícios, uma pessoa de 75 kg levanta seu peso inteiro na ponta de um pé (Figura P11.59). O tendão de Aquiles puxa diretamente para cima no osso do calcanhar do seu pé. Esse tendão tem 25 cm de comprimento, uma área reta de 78 mm2 e módulo de Young de 1.470 MPa. (a) Desenhe um diagrama do corpo livre do pé da pessoa (tudo abaixo do tornozelo). Ignore o peso do pé. (b) Que força é exercida pelo tendão de Aquiles sobre o calcanhar durante esse exercício? Expresse sua resposta em newtons e em múltiplos do peso da pessoa. (c) Em quantos milímetros o exercício estica o tendão de Aquiles?
Passo 1
E aii galera, vamos fazer mais uma questão?
Letra a:
O diagrama de corpo livre é mostrado abaixo. Onde o tendão de Aquiles exerce uma força de tensão T com a seta vermelha e o centro da massa do pé é representado pelo pivô e os dedos exercem uma força normal N.
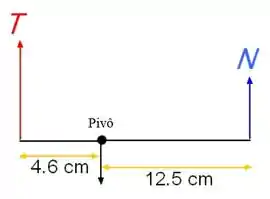
Passo 2
Letra b:
O torque no pé é zero pois está em equilíbrio.
Tanto as forças normais quanto as de tensão fazem o equilíbrio e fazem o torque zero, então podemos obter a força de tensão T, temos:
Sendo , então:
tensão é 2,72 vezes o peso da pessoa. Porque
Passo 3
Letra c:
A equação (11.10) afirma o módulo de Young na forma:
Agora, resolvemos esta equação:
Resposta
- Ver diagrama
- . 2,72 vezes o peso da pessoa