Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 9
Uma régua de um metro está em equilíbrio horizontal sobre a lâmina de uma faca na marca de . com duas moedas de empilhadas na marca de , a régua fica em equilíbrio na marca de . Qual é a massa da régua?
Passo 1
Fala galerinha bonita, tudo belezinha?
Saca só, vamos imaginar o que acontece no problema, chamando de , as forças que a faca e a moeda exercem sobre a régua:
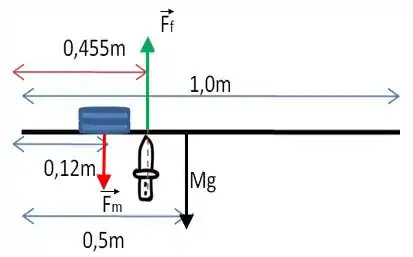
Vamos também chamar de a massa do conjunto das duas moedas e de a massa da régua!
E repara no desenho, que o peso da régua () é aplicado no centro da régua, há uma distância de 0,5m da extremidade.
Passo 2
Agora, vamos analisar o equilíbrio de torques que a e o peso da régua exercem sobre o ponto onde é aplicada a força da faca. Repare que não exerce torque, pois ela está sobre o eixo de rotação que consideramos (ponta da faca). Fazendo o equilíbrio de torques com relação ao ponto de aplicação da faca, temos:
O que nos dá:
Passo 3
Estamos quase lá! Para calcularmos , basta sabermos o valor de Mas nós temos esse valor, pois ele é o peso das duas moedas de :
Substituido esse valor na última equação do passo 2, temos:
Portanto: