Você precisa medir a massa M de uma barra longa de 4,00 m. A barra tem uma seção reta, mas alguns furos feitos ao longo de sua extensão, e você suspeita que seu centro de gravidade não está no meio da barra, a qual é muito grande para você pesar na sua balança. Assim, primeiro você equilibra a barra em um pivô tipo ponta de faca e determina que o centro de gravidade da barra está a 1,88 m de sua extremidade esquerda. Depois você coloca a barra no pivô de modo que o ponto de suporte esteja a 1,50 m da extremidade esquerda da barra. Em seguida, suspende uma massa de 2,00 kg (m1) a partir da barra em um ponto a 0,200 m da extremidade esquerda. Por fim, você suspende uma massa m2 1,00 kg a partir da barra a uma distância x da extremidade esquerda e ajusta x de modo que a barra fique equilibrada. Essa etapa é repetida para outros valores de m2 e você registra cada valor correspondente de x. A tabela a seguir mostra os resultados obtidos.

(a) Desenhe um diagrama do corpo livre para a barra quando m1 e m2 forem suspensos dela. (b) Aplique a equação do equilíbrio estático gtz 0 com o eixo no local do pivô. Resolva a equação para x como uma função de m2. (c) Desenhe x versus 1/m2. Use a inclinação da linha de melhor ajuste e a equação derivada no item (b) para calcular a massa M da barra. Use g 9,80 m/s2 . (d) Qual é a interceptação y da linha reta que se encaixa aos dados? Explique por que tem esse valor.
Passo 1
E aiiiiiiiii galera, tudo bom com vocês?
Vamos fazer mais uma questão!!
Letra a:
Temos o diagrama de corpo livre a seguir:
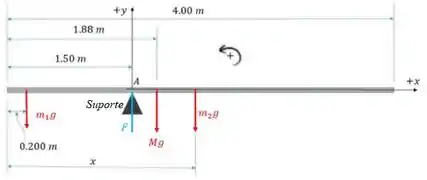
Passo 2
Letra b:
Equacionando:
Passo 3
Letra c:
Vamos agora fazer o gráfico
![]()
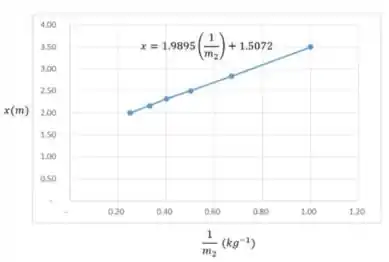
Compare as equações encontradas na Parte (b) com a equação encontrada no gráfico linear.
Comparando:
Passo 4
Letra d:
Quanto maior o , menos é o x.
A interseção está em x = 150m. está suspenso no suporte e pode assumir qualquer valor.
A barra não será equilibrada e girará no sentido anti-horário em torno de A.
Da questão B, temos:
Resposta
Ver resolução