Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 25.4 - Ex. 34
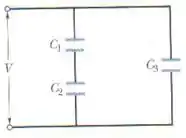
Na figura, uma diferença de potencial V = 100 V é aplicada a um circuito de capacitores cujas capacitâncias são = 10,0 μF, = 5,00 μF e = 4,00 μF. Determine (a) ; (b) ; (c) a energia armazenada ; (d) ; (e) ; (f) ; (g) ; (h) ; (i) .
Passo 1
Falaaaaa galerinhaaa!! Essa é para aquelas pessoas que amam uma continhaa!!
Na letra (a) nós queremos achar a carga armazenada no capacitor 3, certo?
Se lembram da fórmula?
Sabemos que:
Substituindo na fórmula:
A letra (b) nós já até respondemos, certo?
Pelo desenho fica fácil da gente ver que O capacitor 3 está sujeito à tensão V, então:
Ainda para o capacitor 3 nós queremos achar a energia armazenada, .
Se lembram da fórmula que usamos aqui?
Substituindo fica fácil:
Até aqui tranquilo, vamos seguindo !!
Passo 2
Nas letras (d), (e) e (f) nós queremos achar , e !!
Pra achar a gente precisa achar a capacitância equivalente entre 1 e 2 que estão em série, se lembram da fórmula?
O capacitor e não possuem o mesmo potencial, mas a carga permanece a mesma!! Então vamos usar a fórmula para achar a carga equivalente:
Aqui nós já respondemos a letra (d) e a (g) !!
Agora que temos e já sabemos podemos usar a mesma fórmula e achar
E para finalizar:
Estamos quase no fim !!
Passo 3
Já achamos a letra (g), mas ainda precisamos achar e !!
A fórmula é a mesma:
E para finalizar:
Chegamos ao fim de mais uma !!
Resposta
Letra (a):
Letra (b):
Letra (c):
Letra (d):
Letra (e):
Letra (f):
Letra (g):
Letra (h):
Letra (i):