Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 17.5 - Ex. 21

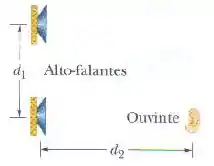
Na figura, dois alto-falantes separados por uma distância d 1 = 2,00   m estão em fase. Suponha que as amplitudes das ondas sonoras emitidas pelos alto-falantes são aproximadamente iguais para um ouvinte que se encontra diretamente à frente do alto-falante da direita, a uma distância d 2 = 3,75   m . Considere toda a faixa de audição de um ser humano normal, 20   H z a 20   k H z . (a) Qual é a menor frequência, f m í n , 1 , para qual a intensidade do som é mínima (interferência destrutiva) na posição do ouvinte? Por que número a frequência f m í n , 1 , deve ser multiplicada para se obter (b) a segunda menor frequência, f m í n , 2 , para a qual a intensidade do som é mínima e (c) a terceira menor frequência, f m í n , 3 , para a qual a intensidade do som é mínima? (d) Qual é a menor frequência, f m á x , 1 , para a qual a intensidade do som é máxima (interferência construtiva) na posição do ouvinte? Por qual número f m á x , 1 deve ser multiplicada para se obter (e) a segunda menor frequência, f m á x , 2 , para a qual a intensidade do som é máxima, e (f) a terceira menor frequência, f m á x , 3 , para a qual a intensidade do som é máxima?

Passo 1

Beleza, essa é uma questão longa, mas é muito importante. Vamos ver as informações que já temos.

São dois alto-falantes separados por uma distância d 1 = 2,00   m , e tem um ouviente em frente a um dos alto-falantes, a uma distância d 2 = 3,75   m .

De cara seria uma boa a gente achar a distância entre o ouvinte e o alto-falante de cima, concorda? Vamos chamar isso de d 3 e usar o teorema de Pitágoras:

d 3 = d 1 2 + d 2 2

d 3 = 2 2 + 3,75 2

d 3 = 4,25   m

A outra coisa que sabemos, porque o livro pede pra usarmos isso ao longo do capítulo, é a velocidade do som.

v = 343   m / s

Ok, vamos em frente.

Passo 2

(a) Ouviu falar em interferência? Pense logo nessa fórmula aqui:

ϕ = Δ L λ ( 2 π )

E em seguida, ouviu falar em interferência destrutiva? Lembre que ela acontece quando essa diferença de fase ϕ é um múltiplo ímpar de π , ou seja:

ϕ = Δ L λ 2 π = 2 n + 1 π

Com n = 0 ,   1 ,   2 ,   …

Ah, outra coisa. Todas as perguntas são sobre frequência, então vamos usar essa fórmula aqui pra fazer a frequência aparecer aí no meio:

v = λ f

1 λ = f v

Substituindo isso na fórmula de cima:

Δ L λ 2 π = 2 n + 1 π

Δ L f v 2 π = 2 n + 1 π

Arrumando um pouco:

f = 2 n + 1 ( v ) π ( 2 π ) ( Δ L )

f = 2 n + 1 ( v ) ( 2 ) ( Δ L )

Beleza, essa é a nossa fórmula para as frequências que geram interferência destrutiva!

Passo 3

(a) Agora fica fácil, os valores de n são simplesmente:

n = 0 ,   1 ,   2 ,   3 ,   …

Então a menor frequência destrutiva vai ser o caso n = 0 .

Então vamos substituir esse e os outros valores na nossa fórmula.

f = 2 n + 1 ( v ) ( 2 ) ( Δ L )

A diferença de percurso Δ L vai ser a diferença entre aquelas distâncias que nós já calculamos:

f m í n , 1 = ( 2 0 + 1 ) ( 343 ) ( 2 ) ( d 3 - d 2 )

f m í n , 1 = ( 343 ) ( 2 ) ( 4,25 - 3,75 ) = 343 ( 2 ) ( 0,5 ) = 343   H z

Passo 4

(b) E agora a segunda menor frequência destrutiva vai ser simplesmente o n = 1 :

f m í n , 2 = ( 2 n + 1 ) ( 343 ) ( 2 ) ( 4,25 - 3,75 ) = 3 343 = 1029   H z

Ou seja, a frequência deve ser multiplicada por 3 .

E você já deve imaginar como vai ficar a letra (c).

Passo 5

(c) Agora é só fazer o caso n = 2 .

f m í n , 3 = ( 2 n + 1 ) ( 343 ) ( 2 ) ( 4,25 - 3,75 ) = 5 343 = 1715   H z

Ou seja, a frequência deve ser multiplicada por 5.

Passo 6

(d) Agora antes de fazer praticamente a mesma coisa para as frequências construtivas, vamos achar a nova fórmula geral.

A única diferença é que ao invés de pegar os múltiplos ímpares de π , nós vamos pegar todos os múltiplos de 2 π . Ou seja:

Δ L f v 2 π = n 2 π

n =   1 ,   2 ,   3 ,   …

Agora arrumando um pouco:

f = n ( v ) π ( π ) ( Δ L )

E já vamos colocar logo o valor de Δ L = 4,25 - 3,75 = 0,5

f = n ( v ) π ( 0,5 ) ( π )

Cortando o π e lembrando que 0,5 = 1 / 2 :

f = n 2 v = n ( 686 )

Agora vamos lá.

Passo 7

(d) A menor frequência construtiva vai ser o caso n = 1 . (Pulamos o zero porque ele corresponde à ausência de uma onda, aí não serve)

f m á x , 1 = 1 686 = 686   H z

Passo 8

(e) A segunda menor frequência construtiva vai ser o caso n = 2 .

f m á x , 2 = 2 686 = 1372   H z

Ou seja, temos que multiplicar a frequência de cima por um fator igual a 2 .

Passo 9

(f) A terceira menor frequência construtiva vai ser o caso n = 3 .

f m á x , 3 = 3 686 = 2058   H z

Ou seja, temos que multiplicar a frequência de cima por um fator igual a 3 .

Resposta

(a) f m í n , 1 = 343   H z

(b) Fator 3 .

(c) Fator 5 .

(d) f m á x , 1 = 686   H z

(e) Fator 2 .

(f) Fator 3 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura mostra quatro fontes sonoras pontuais isotrópicas uniformemente espaçadas ao longo de um eixo x . As fontes emitem sons de mesmo comprimento de onda λ e mesma amplitude s m e estão em fase. U
Na figura, as ondas sonoras A e B , de mesmo comprimento de onda λ , estão inicialmente em fase e se propagam para a direita, como indicam os dois raios. A onda A é refletida por quatro superfícies, m
A figura mostra duas fontes sonoras pontuais isotrópicas, F 1 e F 2 . As fontes, que emitem ondas em fase, de comprimento de onda λ = 0,50m , estão separadas por uma distância D = 1,75m . Se um detect
Na figura, dois alto-falantes separados por uma distância d 1 = 2,00m estão em fase. Suponha que as amplitudes das ondas sonoras emitidas pelos alto-falantes são aproximadamente iguais para um ouvinte
A figura mostra duas fontes pontuais F 1 e F 2 que emitem sons de comprimento de onda λ = 2,00m . As emissões são isotrópicas e em fase; a distância entre as fontes é d = 16,0m . Em qualquer ponto P s