Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.5 - Ex. 59
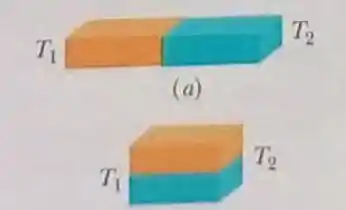
Na Figura, duas barras retangulares metálicas de mesmas dimensões e feitas da mesma substância são soldadas pelas faces de menor área e mantidas a uma temperatura do lado esquerdo e a uma temperatura do lado direito . Em 2,0 min,
são conduzidos a uma taxa constante do lado direito para o lado esquerdo. Que tempo seria necessário para conduzir se as placas fossem soldadas pelas faces de maior área, como na Figura?
Passo 1
O “segredo” dessa questão é a gente enxergar de cara que a potência de condutividade é proporcional à razão (área/comprimento), pois:
Em que e são respectivamente as temperaturas de cada extremidade, na ordem inversa ao sentido do fluxo de calor.
Primeiro, vamos entender os dois casos separadamente, ok?
A situação em (a) é:
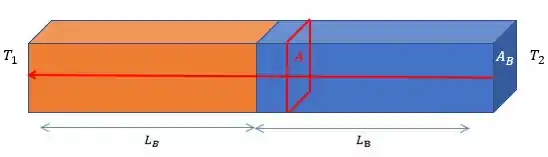
O calor passa de para , pois está mais quente. Além disso, temos que é a área da base das placas e é o comprimento delas.
Agora, repare que na fórmula para a potência, nossa área será e o comprimento . Então, em (a), nossa fórmula para a potência é:
Já em (b):
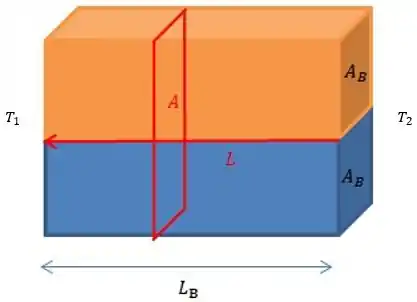
O calor continua passando no mesmo sentido! A diferença é que nossa área, agora, é e nosso comprimento . Logo, nossa fórmula em (b) fica:
Você pode ver que as únicas coisas que mudam entre as duas situações são a área e o comprimento. Pois as temperaturas finais e iniciais são iguais, além da condutividade também ser, já que não mudamos o material, show?
Passo 2
Se tirarmos a razão entre as potências, podemos saber a razão entre os tempos que vão demorar em cada situação:
E, então, podemos simplificar o , , e :
Arrumando isso:
Consequentemente, no caso (b) seria necessário um tempo de para que a mesma quantidade de calor passe pelas placas soldadas, pois sua potência é 4 vezes maior que a potência em (a). Não acredita em mim? Vou te mostrar!
Passo 3
O enunciado nos deu que em passaram na situação (a). O que nos dá uma potência de:
Substituindo na fórmula do passo anterior:
Passo 4
Como vimos, a potência é calculada pela energia dividida pelo tempo. No caso (b), queremos saber quanto tempo demoraria para passarem os . A fórmula fica assim, então:
E já calculamos quanto é essa potência:
E , então: . Esse é o tempo que demoraria em (b). Show?