Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 2.Exercícios e Problemas - Ex. 9

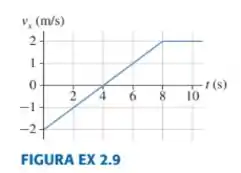
A FIGURA EX 2.9 mostra o gráfico da velocidade de um trem que parte da origem em t =   0   s .

  1. Determine a aceleração do trem em t = 3,0   s .
  2. Trace os gráficos da posição e da aceleração para o trem.

Passo 1

  1. Determine a aceleração do trem em t = 3,0   s .

    2. Bom, temos o gráfico da velocidade versus tempo e queremos saber a aceleração.

    Vamos lembrar de algo muito importante:

    EM UM GRÁFICO DE VELOCIDADE VERSUS TEMPO A ACELERAÇÃO É IGUAL A INCLINAÇÃO DA RETA

    O que vamos fazer é calcular a inclinação da reta que descreve o movimento em t = 3 s e assim conseguimos achar a aceleração.

    Passo 2

    A inclinação de uma reta ( α ) é calculada da seguinte maneira:

    α = ∆ y ∆ x

    Em um gráfico de velocidade versus tempo, o nosso y é a velocidade, o x é o tempo e a inclinação da reta é a aceleração, então temos que:

    a = ∆ v ∆ t =   v f - v i t f - t i

    Para o intervalo de tempo 0 ≤ t ≤ 8 , teremos:

    a =   2 - ( - 2 ) 8 - 0 = 4 8 = 0,5   m / s 2

    O tempo t = 3 s pertence a esse intervalo, então a aceleração nesse tempo também é 0,5   m / s 2 .

    Passo 3

  2. Trace os gráficos da posição e da aceleração para o trem.

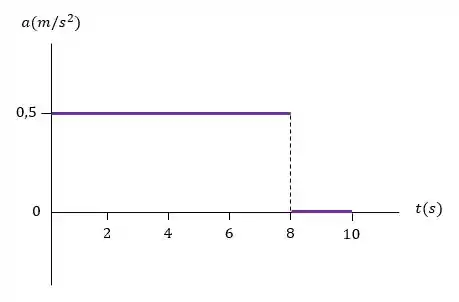
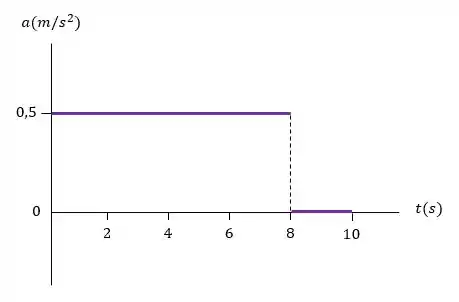
Primeiro vamos fazer o gráfico da aceleração versus tempo:

Vimos que para o intervalo 0 ≤ t ≤ 8 , temos:

a = 0,5   m / s 2

Vamos fazer a mesma conta para o intervalo seguinte 8 ≤ t ≤ 10 :

a = 2 - 2 10 - 8 = 0   m / s 2

Agora, com os valores obtidos para a aceleração em cada intervalo de tempo vamos construir o gráfico:

Passo 2

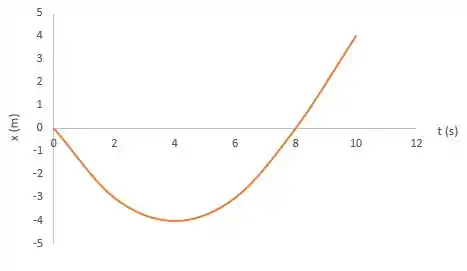
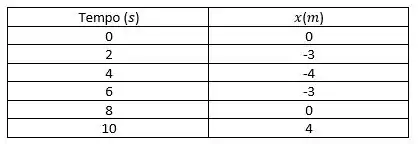
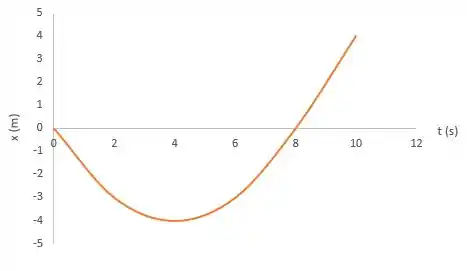
Agora, vamos construir o gráfico da posição versus tempo.

Para construir esse gráfico precisamos ter em mente uma informação super importante:

A ÁREA DO GRÁFICO VELOCIDADE VERSUS TEMPO NOS FORNECE A DISTÂNCIA PERCORRIDA PELA PARTÍCULA

Guarda isso no coração, combinado?

Então para calcular a posição da partícula em determinado instante devemos seguir essa fórmula:

x f = x 0 + d i s t â n c i a   p e r c o r r i d a

x f = x 0 + á r e a   d o   g r á f i c o   e n t r e   t 0   e   t f

Passo 3

A questão disse que a partícula parte da origem, então:

x 0 = 0   m

Vamos usar a fórmula do passo 4 para achar a posição em cada instante de tempo, beleza?

Para t = 2 s

x 2 s = 0 - á r e a   d o   g r á f i o   e n t r e   0 s   e   2 s

Fica muito atento que áreas que estão abaixo do eixo x do gráfico são subtraídas e área acima são somadas, okay?

x 2 s = 0 - 1 2   . 2.1 + 2.1 =   - 3   m  

Vamos aplicar essa fórmula para os demais instantes:

Para t = 4 s

x 4 s = 0 - á r e a   d o   t r i â n g u l o   e n t r e   0 s   e   4 s

x 4 s = 0 - 1 2   . 2.4 =   - 4   m

Para t = 6 s

x 6 s = 0 - á r e a   d o   t r i â n g u l o   e n t r e   0 s   e   4 s + ( á r e a   d o   t r i â n g u l o   e n t r e   4 s   e   6 s )

x 6 s = 0 - 4   + 1 2   .   2.1   = - 4 + 1 = - 3   m

Para t = 8 s

x 8 s = 0 - á r e a   d o   t r i â n g u l o   e n t r e   0 s   e   4 s + ( á r e a   d o   t r i â n g u l o   e n t r e   4 s   e   8 s )

x 8 s = 0 - 4 + 1 2   .   4.2   =   0   m

Para t = 10 s

x 10 s = 0 - á r e a   d o   t r i â n g u l o   e n t r e   0 s   e   4 s + á r e a   d o   t r i â n g u l o   e n t r e   4 s   e   8 s + ( á r e a   d o   r e t â n g u l o   e n t r e   8 s   e   10 s )

x 10 s = 0 - 4 +   4 + 2.2   =   4   m

Agora, com essas informações podemos montar o gráfico:

Resposta

  1. A aceleração em t = 3 s é a = 0,5   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um avião a jato de grande porte precisa atingir a velocidade de 500km/h para decolar, e tem uma aceleração de 4 m / s 2 . Quanto tempo ele leva para decolar e que distância percorre na pista até a dec
Um jato comercial deve atingir uma velocidade de 360k m / h para decolar. Qual é o menor aceleração constante necessária para que o avião decole de uma pista com 1,80k m de extensão?
A FIGURA EX 2.10 mostra o gráfico da velocidade de uma partícula que se move sobre o eixo x . Sua posição inicial é x 0 =2,0m em t 0 =0s . Em t = 2,0s , quala posição da partícula,sua velocidade esua
Na FIGURA EX 2.11 é mostrado o gráfico da velocidade versus tempo de uma partícula que se move ao longo do eixo x . Sua posição inicial é x 0 =2,0m em t 0 =0s .Quanto valem a posição, a velocidade e a
A FIGURA EX 2.8 mostra o gráfico da velocidade de uma partícula. Trace o gráfico da aceleração da partícula para o intervalo 0 s≤t≤4s . Escolha uma escala numérica apropriada para cada eixo.